III. Navigation réactive▲
Dans cette partie, nous présentons différentes stratégies de navigation réactive. Ces stratégies peuvent être utilisées dans des architectures de contrôle purement réactives, mais aussi comme modules de bas niveau dans une architecture hybride. Par définition, les stratégies de navigation réactives n'utilisent que les valeurs courantes des capteurs (ou des valeurs sur une petite fenêtre temporelle) et non des données provenant d'un modèle interne, pour décider de l'action à effectuer.
III-A. Navigation vers un but▲
Nous commençons ici par des méthodes de navigation correspondant aux deux premières catégories de stratégies de navigation définies dans le chapitre I.ATypes de navigation, c'est-à-dire l'approche d'un but défini par un objet ou une configuration d'amers.
III-A-1. Véhicules de Braitenberg▲
Dans son livre « Vehicles: Experiments in Synthetic Psychology », Valentino Braitenberg [19] décrit une série d'expériences dans lesquelles des robots extrêmement simples peuvent montrer des comportements complexes, qu'un observateur humain associe en général à différents types d'émotions telles que la peur ou l'agression. Nous nous intéressons ici simplement à la structure de ces robots, qui permet de réaliser simplement des comportements pour rejoindre un but visible. Cette structure est devenue l'archétype des méthodes réactives simples.
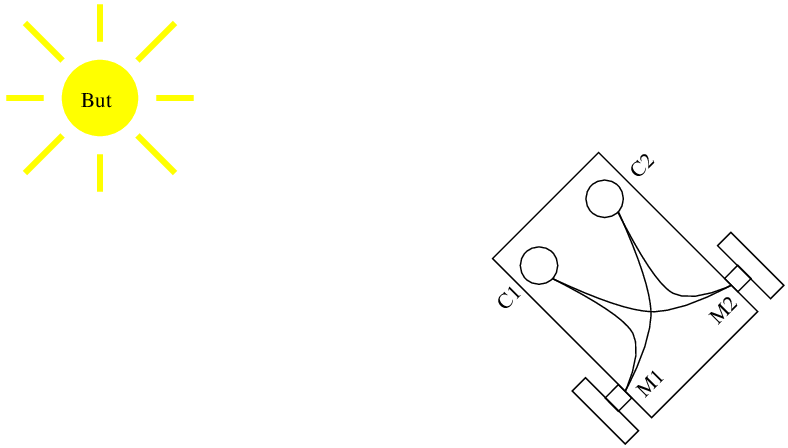
Dans le livre de Braitenberg, le but est matérialisé par une lumière, visible depuis tout l'environnement. Le robot est simplement une plate-forme différentielle, constituée de deux roues dont on commande les vitesses de rotation et munie de deux capteurs de lumière situés de part et d'autre de l'avant du robot (Figure 5.1). L'architecture interne du robot est simplement constituée de liens entre ces capteurs et les moteurs qui permettent de calculer la vitesse des moteurs en fonction des valeurs des capteurs.
En faisant varier les paramètres des connexions, il est alors possible de définir différents comportements du robot. Si la vitesse de chaque moteur est reliée à la valeur du capteur du côté opposé avec un coefficient positif, le robot se dirigera naturellement vers le but. Si, par contre, la vitesse de chaque moteur est reliée à la valeur du capteur du même côté avec un coefficient positif, le robot fuira le but.
Ces véhicules réalisent simplement une remontée ou une descente de gradient sur l'intensité de la lumière. Ils correspondent à un simple contrôleur proportionnel en automatique et sont donc relativement sujets à des oscillations dans le comportement du robot. Ils supposent de plus que le but est visible depuis tout l'environnement, ce qui est rarement le cas en pratique. Ce modèle est donc intéressant, car c'est la méthode la plus simple possible pour réaliser un déplacement vers un but, mais il est difficile à utiliser dans une application réelle.
III-A-2. Modèle de Cartwright et Collet▲
Le « snapshot model » a été conçu pour expliquer comment des abeilles peuvent utiliser des informations visuelles pour rejoindre un point donné de l'environnement. Il permet à un robot de rejoindre un but dont la position est définie par la configuration d'amers de l'environnement autour de ce but.
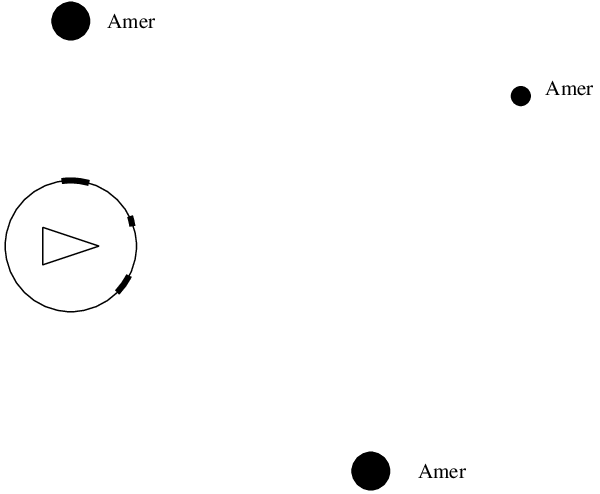
Le système perceptif du robot doit lui permettre de détecter la direction et la taille des amers autour de lui. Le robot commence par mémoriser le but en enregistrant la configuration des amers vus depuis la position de ce but (un snapshot, Figure 5.2).

Lorsque, par la suite, le robot veut rejoindre ce but, il prend une nouvelle image des amers et, par comparaison entre la configuration courante et la configuration mémorisée au but, il peut déduire de manière très simple la direction dans laquelle se déplacer pour atteindre le but. Cette comparaison est basée sur un appariement entre les amers perçus et les amers mémorisés, chaque appariement permettant de calculer un vecteur dont la somme, pour tous les appariements d'amers, donne la direction à prendre pour rejoindre le but (Figure 5.3). Le robot effectue alors un déplacement de longueur fixée dans cette direction puis recommence le processus tant que le but n'est pas atteint.
Là encore, le système est très simple et réalise une descente de gradient sur la configuration des amers afin d'atteindre le but. Il ne fonctionne cependant pas sur l'ensemble de l'environnement et la qualité du comportement obtenu dépend beaucoup de la configuration des amers qui sont utilisés, un ensemble d'amers lointains et bien répartis tout autour du robot donnant les meilleurs résultats. La qualité de l'appariement entre les amers est également primordiale. En effet, si un amer perçu est associé au mauvais amer mémorisé, le vecteur de déplacement déduit sera faux. Le modèle original supposait des amers noirs sur fond blanc, sans identité particulière, pour lesquels l'appariement est relativement hasardeux. Il n'est donc pas applicable en pratique. D'autres travaux ont utilisé des amers colorés et différentes contraintes sur l'appariement qui permettent une meilleure robustesse et sont donc applicables à des robots réels [58].
La plupart des implantations de ce modèle supposent de plus que la direction du robot soit connue afin de faciliter l'appariement. Avoir une estimation correcte de cette direction peut se révéler difficile en pratique.
III-A-3. Asservissement visuel▲
L'asservissement visuel [30] (document disponible en ligne(4)) est une technique d'asservissement de la position d'un robot qui est basée directement sur l'information extraite d'une image, sans modélisation intermédiaire de l'environnement. Développées à l'origine pour la commande des robots manipulateurs, ces techniques permettent également la commande de robots mobiles.

Dans ces approches, le but à atteindre est spécifié par l'image que le robot devra percevoir depuis cette position. Différentes mesures sont réalisées sur cette image (par exemple la détection de points d'intérêts) et la commande du robot est conçue pour amener à zéro l'écart entre la mesure réalisée sur l'image courante et la mesure réalisée sur l'image cible (Figure 5.4). Les choix de mesures dans l'image et de la loi de commande peuvent être très variés et vont conditionner les trajectoires obtenues par le robot, leur stabilité, leur robustesse aux mauvaises perceptions ou aux mauvaises modélisations du système, etc.
Nous ne détaillerons pas ici ces approches, mais il existe plusieurs applications intéressantes en robotique mobile [15, 123, 34]. Notons que ces modèles sont souvent étendus pour fournir une navigation à long terme en enchaînant des tâches de contrôle local sur des séquences d'images. Par exemple, [15] présente un système permettant de guider un robot en environnement intérieur à partir du suivi de motifs détectés sur le plafond par une caméra pointée à la verticale. En enchaînant des asservissements sur une séquence d'images, ce système permet au robot de refaire une trajectoire qui a été montrée au préalable par un opérateur. De même, [123] et [34] réalisent le guidage d'un véhicule en extérieur à l'aide d'une caméra pointée vers l'avant.
III-B. Évitement d'obstacles▲
L'évitement d'obstacles est un comportement de base présent dans quasiment tous les robots mobiles. Il est indispensable pour permettre au robot de fonctionner dans un environnement dynamique et pour gérer les écarts entre le modèle interne et le monde réel.
Les méthodes que nous présentons sont efficaces à condition d'avoir une perception correcte de l'environnement. Elles seront par exemple très efficaces avec un télémètre laser, mais donneront des résultats plus bruités avec des sonars. Pour limiter ce problème, il est possible d'appliquer ces méthodes sur une représentation locale de l'environnement (c'est-à-dire de l'environnement proche du robot et centrée sur le robot) qui sera construite en fonction des données de quelques instants précédents. Cette représentation intermédiaire permettra de filtrer une grande partie du bruit des données individuelles (en particulier pour les sonars).
Il faut également faire attention à ce que les capteurs détectent tous les obstacles. Par exemple, un laser à balayage ne verra pas les objets au-dessous ou au-dessus de son plan de balayage et pourra avoir du mal à percevoir les vitres. Pour cette raison, on utilise souvent une nappe laser couplée à des sonars ou un système de plusieurs nappes laser inclinées.
III-B-1. Méthode des champs de potentiel▲

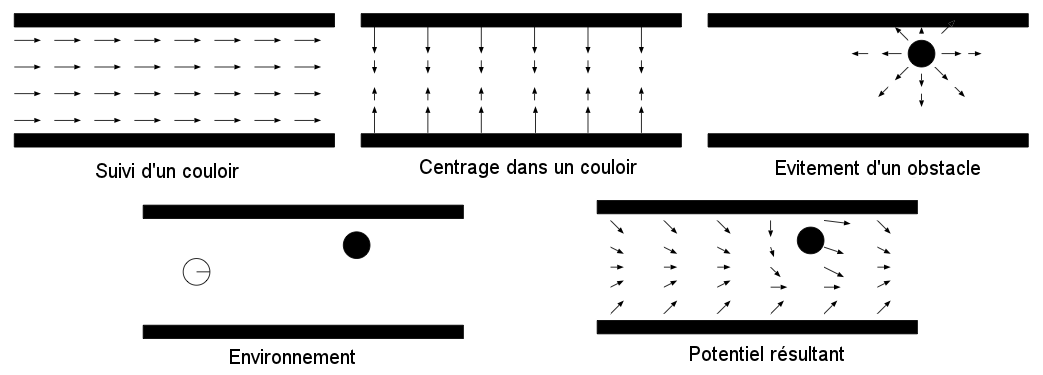
Dans la méthode d'évitement d'obstacles par champs de potentiels, on assimile le robot à une particule se déplaçant suivant les lignes de courant d'un potentiel créé en fonction de l'environnement perçu par le robot. Ce potentiel traduit différents objectifs tels que l'évitement d'obstacles ou une direction de déplacement préférée. Il est calculé par sommation de différentes primitives de potentiels traduisant chacun de ces objectifs (Figure 6.1). Ces différents potentiels peuvent avoir une étendue spatiale limitée ou non (par exemple, n'avoir une influence que près des obstacles) et leur intensité peut dépendre ou non de la distance.
Le gradient de ce potentiel donne, en chaque point de l'espace, la direction de déplacement du robot (Figure 6.1). Comme c'est ce gradient et non la valeur absolue du potentiel qui nous intéresse, il est possible de calculer directement en chaque point sa valeur, par une simple somme vectorielle, en ajoutant les valeurs issues des différents potentiels primitifs. Ainsi, pour un robot se déplaçant en ligne droite en espace ouvert et évitant les obstacles qu'il peut rencontrer, nous obtenons par exemple les lignes de courant illustrées à la Figure 6.2.
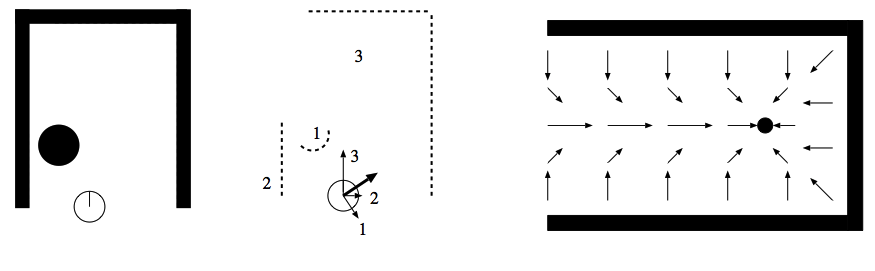
De plus, dans la pratique, pour l'évitement d'obstacles, le potentiel est en général calculé dans l'espace relatif au robot et ne sert qu'à décider de la vitesse et de la direction courante. Il n'est donc nécessaire de l'estimer que pour la position courante du robot, en sommant simplement la contribution des différents éléments perçus (Figure 6.3).
Le principal inconvénient de cette méthode d'évitement d'obstacles est l'existence, pour certaines configurations d'obstacles (relativement courantes), de minimums locaux du potentiel qui ne permettent pas de décider de la direction à prendre (Figure 6.3). Ce problème peut être traité de différentes façons. Il est par exemple possible de déclencher un comportement particulier lorsque l'on rencontre un tel minimum (déplacement aléatoire, suivi de murs…). Il est aussi possible d'imposer que le potentiel calculé soit une fonction harmonique, ce qui garantit qu'il n'ait pas de minima, mais rend son estimation beaucoup plus lourde en calcul.
Le principe de ces champs de potentiels est formalisé sous le nom de schéma moteur par R. Arkin [4]. Pour lui, un schéma moteur est une action définie sous forme de potentiel en fonction des perceptions du robot. Ces schémas sont utilisés comme contrôleur de bas niveau dans une architecture hybride.
III-B-2. Méthode Vector Field Histogram▲

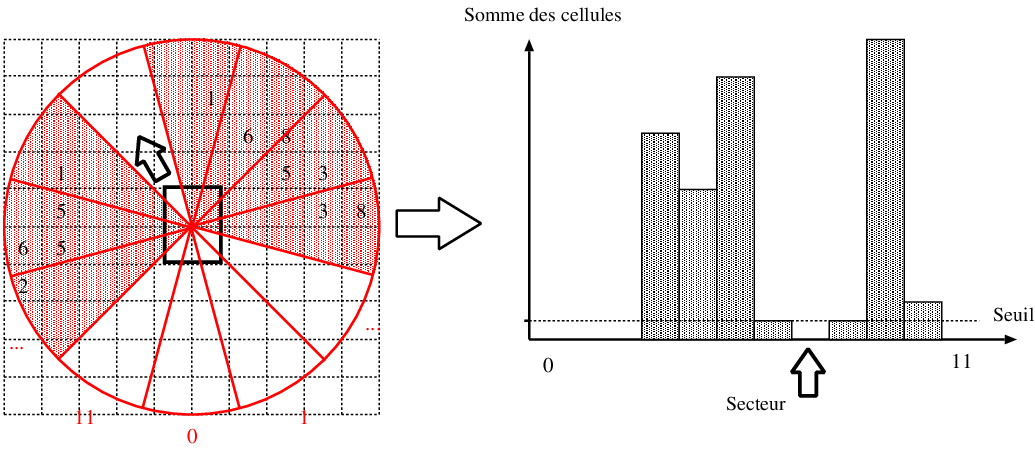
La méthode « Vector Field Histogram » [17] a été conçue spécifiquement pour utiliser une grille d'occupation locale construite à partir de capteurs à ultrasons. Cette grille est construite de manière très rapide par la méthode « Histogrammic in motion mapping » (voir section III.D.2.cCartes métriques : grilles d'occupation) qui produit une grille dont chaque cellule contient un nombre d'autant plus élevé qu'elle a souvent été perçue comme contenant un obstacle (Figure 6.4 haut).
Un histogramme représentant l'occupation de l'environnement autour du robot est ensuite construit à partir de cette grille d'occupation locale. Pour cela, l'environnement est discrétisé en secteurs angulaires pour lesquels la somme des valeurs des cellules est calculée (figure 6.4 bas). Un seuil permettant de tolérer un certain bruit est ensuite utilisé pour déterminer les directions possibles pour le robot : toutes les directions dont la valeur est inférieure au seuil sont considérées. Le choix de la direction est finalement réalisé parmi les directions possibles en fonction de contraintes externes (par exemple la direction la plus proche de la direction du but).
Cette méthode est extrêmement rapide (elle fonctionne sur un PC 386 à 20 MHz !) et a permis historiquement un déplacement réactif à des vitesses assez élevées (environ 1 m/s). Diverses améliorations pour permettre le réglage de la vitesse du robot en fonction de la densité des obstacles ou de la largeur de l'espace angulaire libre sont possibles.
III-B-3. Méthode de la fenêtre dynamique▲
La méthode de la fenêtre dynamique [47] permet de sélectionner une trajectoire locale du robot qui va éviter les obstacles et dont les variations dans le temps vont respecter des contraintes telles que les capacités de freinage maximales du robot. Pour appliquer l'algorithme, les trajectoires locales sont paramétrées et peuvent prendre des formes différentes en fonction par exemple des contraintes d'holonomie du robot. Une méthode simple, applicable à de nombreuses plates-formes, est d'utiliser les vitesses de translation et de rotation du robot.
La méthode de la fenêtre dynamique permet donc, à partir de la perception locale de l'environnement, de sélectionner un couple kitxmlcodeinlinelatexdvp(v,\omega)finkitxmlcodeinlinelatexdvp de vitesses de translation et de rotation du robot qui répond à différentes contraintes, dont celle d'éviter les obstacles. Un tel couple de vitesses, lorsqu'il est appliqué au robot, produit une trajectoire circulaire, pour laquelle la satisfaction des différentes contraintes peut être évaluée. À l'issue de l'évaluation de toutes les contraintes pour tous les couples de vitesses possibles, la méthode de la fenêtre dynamique permet de sélectionner le couple le plus pertinent (qui répond le mieux aux contraintes).
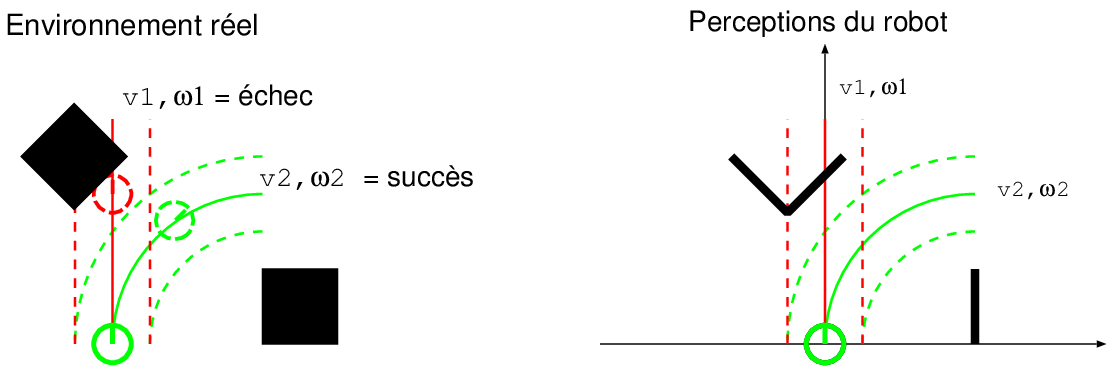
La première contrainte est la contrainte d'évitement d'obstacles. C'est une contrainte dure au sens ou elle est binaire (succès / échec) et doit obligatoirement être satisfaite. Elle est évaluée pour chacune des trajectoires possibles à partir de la perception locale de l'environnement à un instant donné et de la position estimée du robot à un pas de temps fixé dans le futur pour la trajectoire courante. Si le robot n'a pas rencontré d'obstacles à cet horizon, la contrainte est respectée ; dans le cas contraire, elle ne l'est pas (Figure 6.5).
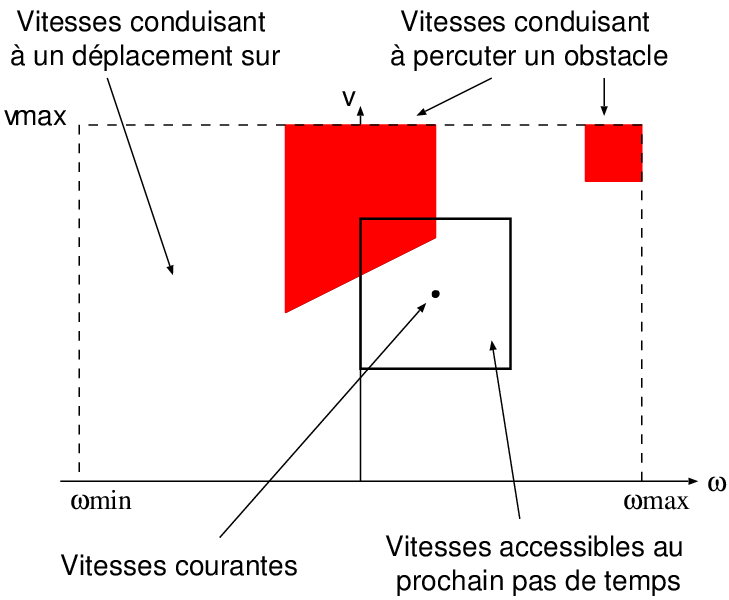
Le respect ou le non-respect de cette contrainte est reporté dans un graphe des vitesses qui indique, pour chaque couple de vitesses possible (donc chaque trajectoire), si le robot va ou ne va pas rencontrer un obstacle (Figure 6.6). Dans ce graphe, il est alors possible de tracer la fenêtre des vitesses accessibles au prochain pas de temps à partir des vitesses courantes du robot et des valeurs d'accélération et décélération maximales. C'est cette fenêtre qui donne son nom à la méthode, car elle permet de prendre en compte la dynamique du robot (à travers la capacité de freinage et d'accélération). Il reste alors à choisir, au sein de cette fenêtre, un couple de vitesses qui ne conduise pas à percuter un obstacle pour garantir un déplacement sûr du robot.
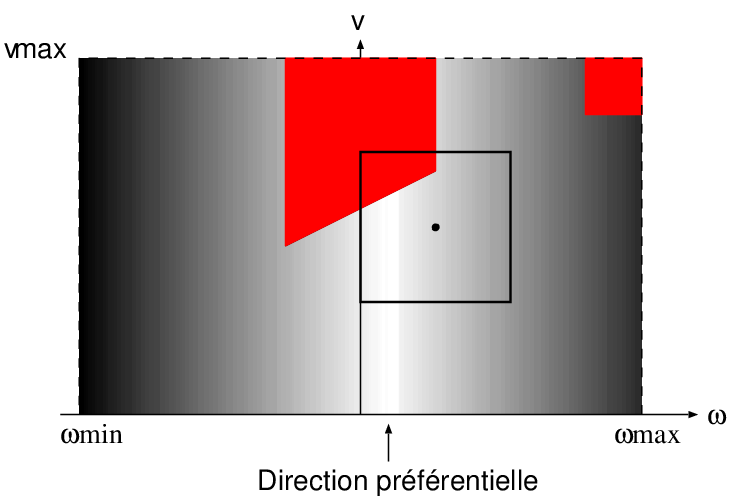
Pour faire le choix parmi toutes les vitesses possibles au sein de cette fenêtre, il est possible d'utiliser des contraintes « souples » supplémentaires pour exprimer des préférences au sein de cet espace des vitesses accessibles. Ces contraintes s'expriment par une fonction de coût kitxmlcodeinlinelatexdvpG(v,\omega)finkitxmlcodeinlinelatexdvp qui est en général la somme de plusieurs termes. Ces termes peuvent exprimer une préférence a priori sur les vitesses, une préférence pour les trajectoires s'éloignant le plus des obstacles, ou une préférence de direction si l'on dispose par exemple d'une estimation de la direction d'un but à long terme (Figure 6.7). Le couple de vitesses minimisant ce coût au sein de la fenêtre est alors sélectionné. Il garantit un déplacement sans rencontrer d'obstacles et le meilleur respect possible des contraintes souples dans ce cadre.
Dans la pratique, les valeurs des différentes contraintes sont évaluées en différents points du graphe des vitesses, le nombre de points dépendant notamment de la puissance de calcul disponible et de la complexité de l'évaluation de chaque contrainte. L'utilisation de la fenêtre dynamique est très intéressante pour un robot se déplaçant rapidement ou pour un robot ayant des capacités d'accélération et de ralentissement limitées. Elle permet alors de produire un déplacement du robot sûr et régulier. Pour des robots qui ont une forte capacité d'accélération et de décélération (par exemple un robot léger avec de bons moteurs électriques), on peut considérer que toutes les vitesses sont accessibles presque instantanément. Il peut alors être suffisant de ne considérer que la cinématique et non la dynamique, ce qui se traduit par la prise en compte d'un seul point du graphe et non d'une fenêtre. La recherche du couple de vitesses est ainsi simplifiée.
III-C. Apprentissage par renforcement▲
Les méthodes que nous avons vues jusqu'à présent sont des associations entre perceptions et actions conçues par des ingénieurs. Or, il existe des techniques d'apprentissage (notamment l'apprentissage par renforcement) permettant de créer des associations de ce type à partir d'informations d'assez haut niveau sur la tâche à réaliser.
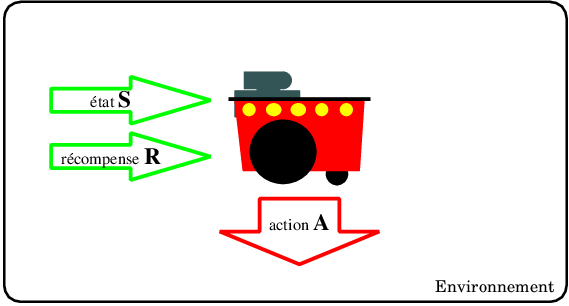
L'apprentissage par renforcement est une méthode qui permet de trouver, par un processus d'essais et d'erreurs, l'action optimale à effectuer pour chacune des situations que le robot va percevoir, afin de maximiser une récompense. C'est une méthode d'apprentissage orientée objectif qui va conduire à un contrôleur optimal pour la tâche spécifiée par les récompenses. Cette méthode est de plus non supervisée, car la récompense ne donne pas l'action optimale à réaliser, mais simplement une évaluation de la qualité de l'action choisie. Elle permet enfin de résoudre les problèmes de récompense retardée pour lesquels il faut apprendre à sacrifier une récompense à court terme pour obtenir une plus forte récompense à long terme et donc apprendre de bonnes séquences d'actions qui permettront de maximiser la récompense à long terme.
Du fait de toutes ces caractéristiques, l'apprentissage par renforcement est une méthode particulièrement adaptée à la robotique.
III-C-1. Formalisation▲
Le problème de l'apprentissage par renforcement pour un agent se formalise à partir des éléments suivants :
- un ensemble d'états kitxmlcodeinlinelatexdvp\mathcal Sfinkitxmlcodeinlinelatexdvp correspondant à la perception que l'agent a de l'environnement ;
- un ensemble d'actions possibles kitxmlcodeinlinelatexdvp\mathcal Afinkitxmlcodeinlinelatexdvp ;
- une fonction de récompense kitxmlcodeinlinelatexdvpR:\{\mathcal S,\mathcal A\} \to \mathbb{R}finkitxmlcodeinlinelatexdvp.
L'agent va interagir avec son environnement par pas de temps discrets, en percevant l'état de l'environnement kitxmlcodeinlinelatexdvps_{t}finkitxmlcodeinlinelatexdvp, en choisissant une action kitxmlcodeinlinelatexdvpa_tfinkitxmlcodeinlinelatexdvp en fonction de cet état et en recevant la récompense kitxmlcodeinlinelatexdvpr_{t+1}finkitxmlcodeinlinelatexdvp associée (Figure 7.1).
L'évolution du robot dans son environnement est régie par un Processus de Décision Markovien (MDP en anglais) qui décrit l'évolution de l'état et de la récompense en fonction des actions du robot. Ce MDP (7.2), qui spécifie complètement la tâche du robot par le jeu des récompenses, se décrit simplement à l'aide de deux fonctions :
- une fonction de transition kitxmlcodeinlinelatexdvp\mathcal P^a_{ss'}=P(s_{t+1}=s'|s_t=s,a_t=a)finkitxmlcodeinlinelatexdvp qui donne la probabilité de passer dans l'état kitxmlcodeinlinelatexdvps'finkitxmlcodeinlinelatexdvp lorsque l'agent effectue l'action kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp dans l'état kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp ;
- une fonction de récompense kitxmlcodeinlinelatexdvp\mathcal R^a_{ss'}=E(r_{t+1}|s_t=s,a_t=a,s_{t+1}=s')finkitxmlcodeinlinelatexdvp qui donne la récompense moyenne lorsque l'agent passe de l'état kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp à kitxmlcodeinlinelatexdvps'finkitxmlcodeinlinelatexdvp en faisant l'action kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp.
Le comportement de l'agent est défini par une politique kitxmlcodeinlinelatexdvp\pi : \{\mathcal S, \mathcal A\} \to [0,1]finkitxmlcodeinlinelatexdvp, qui guide l'agent de manière probabiliste en spécifiant, pour chaque état kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp, la probabilité de réaliser l'action kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp (et donc kitxmlcodeinlinelatexdvp\sum_a \pi(s,a) = 1finkitxmlcodeinlinelatexdvp). Le but de l'apprentissage par renforcement va être de trouver la politique optimale kitxmlcodeinlinelatexdvp\pi^*finkitxmlcodeinlinelatexdvp maximisant la récompense à long terme(5).
La récompense à long terme, que nous appellerons revenu kitxmlcodeinlinelatexdvpR_tfinkitxmlcodeinlinelatexdvp, peut être définie de différentes manières en fonction de la tâche considérée. Si la tâche consiste à répéter des épisodes qui durent un nombre de pas de temps fixe, le revenu pourra être la somme des récompenses instantanées pendant un épisode. Si au contraire la tâche se déroule de manière continue, le revenu pourra se définir comme la somme des récompenses futures pondérées par une exponentielle décroissante :
kitxmlcodelatexdvpR_t = \sum_{k=0}^\infty \gamma^k r_{t+k+1}finkitxmlcodelatexdvpoù kitxmlcodeinlinelatexdvp\gamma \in [0,1]finkitxmlcodeinlinelatexdvp est un facteur indiquant l'importance que l'on accorde aux récompenses futures.
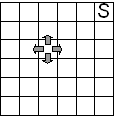
Les algorithmes d'apprentissage par renforcement que nous verrons plus loin utilisent quasiment tous une fonction de valeur kitxmlcodeinlinelatexdvpV^{\pi}finkitxmlcodeinlinelatexdvp (Figure 7.3) qui permet, pour une politique kitxmlcodeinlinelatexdvp\pifinkitxmlcodeinlinelatexdvp donnée, d'estimer le revenu moyen (les récompenses futures) pour un état donné si l'on suit la politique considérée :
kitxmlcodelatexdvpV^{\pi}(s) = E_{\pi}(R_t|s_t=s)finkitxmlcodelatexdvp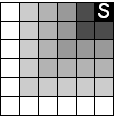
Ces fonctions de valeurs peuvent aussi se définir non pas pour un état, mais pour un état et une action réalisée dans cet état :
kitxmlcodelatexdvpQ^{\pi}(s,a) = E_{\pi}(R_t|s_t=s,a_t=a)finkitxmlcodelatexdvpLa fonction de valeur pour un état kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp étant la moyenne des kitxmlcodeinlinelatexdvpQ^{\pi}(s,a)finkitxmlcodeinlinelatexdvp, pondérée par la probabilité de chaque action :
kitxmlcodelatexdvpV^{\pi}(s) = \sum_a \pi(s,a) Q^{\pi}(s,a)finkitxmlcodelatexdvpUne propriété essentielle de ces fonctions de valeur va permettre de créer les différents algorithmes d'apprentissage, il s'agit de la relation de récurrence connue sous le nom d'équation de Bellman :
kitxmlcodelatexdvpV^{\pi}(s) = \sum_a \pi(s,a) \sum_{s'} \mathcal P^a_{ss'}\left[\mathcal R^a_{ss'} + \gamma V^{\pi}(s')\right]finkitxmlcodelatexdvpCette équation traduit une cohérence de la fonction de valeur en reliant la valeur d'un état à la valeur de tous les états qui peuvent lui succéder . Elle se déduit simplement de la définition de kitxmlcodeinlinelatexdvpv^\pifinkitxmlcodeinlinelatexdvp de la manière suivante :
kitxmlcodelatexdvp\begin{eqnarray*} V^{\pi}(s) &=& E_{\pi}(R_t|s_t=s)\\ &=& E_{\pi}(\sum_{k=0}^\infty \gamma^k r_{t+k+1} |s_t=s)\\ &=& E_{\pi}( r_{t+1} +\gamma\sum_{k=0}^\infty \gamma^k r_{t+k+2} |s_t=s)\\ &=& \sum_a \pi(s,a) \sum_{s'} \mathcal P^a_{ss'}\left[\mathcal R^a_{ss'} + \gamma E_{\pi}\left(\sum_{k=0}^\infty \gamma^k r_{t+k+2} |s_{t+1}=s'\right)\right]\\ &=& \sum_a \pi(s,a) \sum_{s'} \mathcal P^a_{ss'}\left[\mathcal R^a_{ss'} + \gamma V^{\pi}(s')\right] \end{eqnarray*}finkitxmlcodelatexdvpLa fonction de valeur permet de caractériser la qualité d'une politique, elle donne, pour chaque état, le revenu futur si l'on suit cette politique. Elle permet également de comparer les politiques en définissant un ordre partiel :
kitxmlcodelatexdvp\pi \ge \pi' \Leftrightarrow \forall s,V^\pi(s) \ge V^{\pi'}(s)finkitxmlcodelatexdvpCet ordre permet de définir la fonction de valeur de la politique optimale (Figure 7.3) que l'apprentissage par renforcement va chercher à estimer :
kitxmlcodelatexdvpV^\star(s)=\max_\pi V^{\pi}(s)finkitxmlcodelatexdvpfonction qui peut aussi s'exprimer pour un couple état-action :
kitxmlcodelatexdvpQ^\star(s,a)=\max_\pi Q^{\pi}(s,a)finkitxmlcodelatexdvpavec la relation suivante :
kitxmlcodelatexdvpQ^\star(s,a) = E(r_{t+1}+\gamma V^\star(s_{t+1})|s_t=a,a_t=a)finkitxmlcodelatexdvpIl est également possible d'écrire une relation de récurrence pour la fonction de valeur optimale qui sera légèrement différente de l'équation de Bellman. On parle alors d'équation d'optimalité de Bellman, qui peut s'écrire :
kitxmlcodelatexdvp\begin{eqnarray*} V^*(s) & = & \max_{a} E\left(r_{t+1} + \gamma V^*(s_{t+1})|s_t=s,a_t=a\right)\\ & = & \max_{a} \sum_{s'} \mathcal P^a_{ss'}\left[\mathcal R^a_{ss'} + \gamma V^*(s')\right] \end{eqnarray*}finkitxmlcodelatexdvpsoit, pour la fonction kitxmlcodeinlinelatexdvpQfinkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvp\begin{eqnarray*} Q^*(s,a) & = & E\left(r_{t+1} + \gamma \max_{a'}Q^*(s_{t+1},a')|s_t=s,a_t=a\right)\\ & = & \sum_{s'} \mathcal P^a_{ss'}\left[\mathcal R^a_{ss'} + \gamma \max_{a'}Q^*(s',a')\right] \end{eqnarray*}finkitxmlcodelatexdvpIntuitivement, cette équation traduit par l'opérateur kitxmlcodeinlinelatexdvpmax_afinkitxmlcodeinlinelatexdvp, le fait que la politique optimale choisit l'action qui va maximiser le revenu.
Si l'environnement est un MDP fini, ces équations de Bellman ont une solution unique qui va donc donner pour chaque état, la récompense maximale que pourra recueillir l'agent à partir de cet instant. À partir de la connaissance de kitxmlcodeinlinelatexdvpV^*finkitxmlcodeinlinelatexdvp, il est très simple de construire une politique optimale, en associant à chaque état la ou les actions kitxmlcodeinlinelatexdvpa'finkitxmlcodeinlinelatexdvp qui permettent de réaliser le maximum de l'équation d'optimalité de Bellman :
kitxmlcodelatexdvpa' = argmax_{a} E\left(r_{t+1} + \gamma V^*(s_{t+1})|s_t=s,a_t=a\right)finkitxmlcodelatexdvpou, si l'on utilise la fonction kitxmlcodeinlinelatexdvpQfinkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvpa' = argmax_{a} Q^*(s,a)finkitxmlcodelatexdvpIl faut cependant noter que la construction de la politique à partir de kitxmlcodeinlinelatexdvpV^*finkitxmlcodeinlinelatexdvp nécessite la connaissance du modèle du monde afin d'estimer kitxmlcodeinlinelatexdvpr_{t+1}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvps_{t+1}finkitxmlcodeinlinelatexdvp. Cette connaissance est inutile si l'on utilise kitxmlcodeinlinelatexdvpQ^*finkitxmlcodeinlinelatexdvp.
Tout le problème pour l'apprentissage va donc être d'estimer kitxmlcodeinlinelatexdvpV^*finkitxmlcodeinlinelatexdvp ou kitxmlcodeinlinelatexdvpQ^*finkitxmlcodeinlinelatexdvp pour en déduire une politique optimale. On peut remarquer que si l'on connaît complètement le problème (c'est a dire si l'on connaît kitxmlcodeinlinelatexdvp\mathcal P^a_{ss'}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp\mathcal R^a_{ss'}finkitxmlcodeinlinelatexdvp), il est possible de calculer directement kitxmlcodeinlinelatexdvpV^*finkitxmlcodeinlinelatexdvp ou kitxmlcodeinlinelatexdvpQ^*finkitxmlcodeinlinelatexdvp en résolvant le système des équations d'optimalité de Bellman pour chaque état. Cette solution est peu applicable en robotique, car l'environnement est en général inconnu et de plus, elle ne correspond pas à des caractéristiques souhaitables de l'apprentissage tel que la capacité à apprendre par essais et erreurs.
III-C-2. Programmation dynamique▲
La programmation dynamique est un ensemble de méthodes permettant de calculer une politique optimale dans un MDP connu, en utilisant les propriétés des équations de Bellman. Nous supposons donc dans cette section que le modèle de l'environnement est connu. La programmation dynamique va chercher à estimer la fonction de valeur optimale kitxmlcodeinlinelatexdvpV^*finkitxmlcodeinlinelatexdvp afin d'en déduire une politique optimale.
III-C-2-a. Évaluation d'une politique▲
La première étape de la programmation dynamique est l'estimation de la fonction de valeur pour une politique donnée kitxmlcodeinlinelatexdvp\pifinkitxmlcodeinlinelatexdvp. Cela peut se faire soit en résolvant le système des équations de Bellman, soit en utilisant une procédure itérative, que nous préférerons, car elle s'applique plus naturellement, notamment en cas de contraintes temps réel. Cette procédure utilise le fait que la fonction de valeur kitxmlcodeinlinelatexdvpV^\pifinkitxmlcodeinlinelatexdvp est le point fixe de l'équation de Bellman :
kitxmlcodelatexdvpV(s) = \sum_a \pi(s,a) \sum_{s'} \mathcal P^a_{ss'}\left[\mathcal R^a_{ss'} + \gamma V(s')\right]finkitxmlcodelatexdvpNous pouvons ainsi utiliser cette équation comme étape de mise à jour permettant de calculer une suite de fonctions kitxmlcodeinlinelatexdvpV^kfinkitxmlcodeinlinelatexdvp qui convergera vers kitxmlcodeinlinelatexdvpV^\pifinkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvpV^{k+1}(s) = \sum_a \pi(s,a) \sum_{s'} \mathcal P^a_{ss'}\left[\mathcal R^a_{ss'} + \gamma V^k(s')\right]finkitxmlcodelatexdvpLa méthode de programmation dynamique va donc utiliser cette mise à jour tant que les modifications kitxmlcodeinlinelatexdvpmax_s(|V^{k+1}-V^k)finkitxmlcodeinlinelatexdvp seront supérieures à un seuil donné pour fournir une approximation de kitxmlcodeinlinelatexdvpV^\pifinkitxmlcodeinlinelatexdvp.
III-C-2-b. Amélioration d'une politique▲
Après l'évaluation d'une politique, il va être possible d’en calculer une meilleure à partir de sa fonction de valeur associée. En effet, pour une politique donnée, il n'y a aucune raison que la fonction de valeur satisfasse l'équation d'optimalité de Bellman, c'est-à-dire que l'on peut avoir :
kitxmlcodelatexdvp\pi(s) \ne argmax_{a} E\left(r_{t+1} + \gamma V^\pi(s_{t+1})|s_t=s,a_t=a\right)finkitxmlcodelatexdvpPar contre, on peut prouver que la politique kitxmlcodeinlinelatexdvp\pi'finkitxmlcodeinlinelatexdvp définie par :
kitxmlcodelatexdvp\begin{equation} \pi'(s) = argmax_{a} E\left(r_{t+1} + \gamma V^\pi(s_{t+1})|s_t=s,a_t=a\right) \end{equation}\quad(7.1)finkitxmlcodelatexdvpest meilleure ou équivalente à la politique kitxmlcodeinlinelatexdvp\pifinkitxmlcodeinlinelatexdvp, ce qui nous permet d'améliorer notre politique initiale.
De plus, si la politique kitxmlcodeinlinelatexdvp\pi'finkitxmlcodeinlinelatexdvp ainsi définie n'est pas meilleure que kitxmlcodeinlinelatexdvp\pifinkitxmlcodeinlinelatexdvp (c'est-à-dire si kitxmlcodeinlinelatexdvpV^{\pi'} = V^{\pi}finkitxmlcodeinlinelatexdvp), la définition de kitxmlcodeinlinelatexdvp\pi'finkitxmlcodeinlinelatexdvp (eq 7.1) est l'équation d'optimalité de Bellman, qui prouve donc que la politique obtenue est optimale.
III-C-2-c. Algorithmes d'apprentissage▲
L'évaluation et l'amélioration de politique peuvent être utilisées de différentes manières pour estimer une politique optimale pour un MDP donné.
La première méthode, l'itération de politique utilise simplement ces deux phases de manière itérative :
kitxmlcodelatexdvp\pi_0 \rightarrow V^{\pi_0} \rightarrow \pi_1 \rightarrow V^{\pi_1} \ldots \pi^* \rightarrow V^{\pi^*}finkitxmlcodelatexdvpDans ce processus, cependant, l'évaluation de politique est elle-même un processus itératif, qui ne va converger qu'à une erreur donnée près et va de plus être potentiellement un processus très long.
Une autre méthode pour converger vers la politique optimale est d'améliorer la politique avant même d'avoir une estimation correcte de sa valeur. On peut par exemple faire un nombre fixe d'itérations d'évaluation avant de faire une amélioration. Le cas où on ne fait qu'une itération d'évaluation de la politique est l'algorithme d'itération de valeur, pour lequel les deux étapes se réduisent à une seule : kitxmlcodeinlinelatexdvpV^{k+1}(s) = \max_a \sum_{s'} \mathcal P^a_{ss'}\left[\mathcal R^a_{ss'} + \gamma V^k(s')\right]finkitxmlcodeinlinelatexdvp et qui converge vers kitxmlcodeinlinelatexdvpV^*finkitxmlcodeinlinelatexdvp.
Pour les problèmes avec de très grands espaces d'états, le fait de parcourir tous les états pour la mise à jour peut être difficile en soi. Il est dans ce cas possible d'utiliser une méthode de programmation dynamique asynchrone qui réalise la mise à jour de l'itération de valeur pour un état sélectionné au hasard ou en fonction du comportement de l'agent. Cette méthode converge également vers kitxmlcodeinlinelatexdvpV^*finkitxmlcodeinlinelatexdvp, à condition de visiter à la limite tous les états un nombre infini de fois. Elle possède l'avantage de fournir rapidement une approximation de la fonction de valeur.
III-C-3. Méthodes de Monte-Carlo▲
Le fait de devoir connaître l'environnement pour apprendre une stratégie rend les méthodes de programmation dynamique peu utiles en robotique. Les méthodes de Monte-Carlo que nous allons voir dans cette section vont utiliser les mêmes idées (estimer la fonction de valeur puis améliorer la politique), mais en ayant recours à des expériences réalisées dans l'environnement plutôt qu'à un modèle.
III-C-3-a. Évaluation d'une politique▲
L'estimation de la fonction de valeur va se réaliser à partir d'un ensemble de séquences « état-action-récompenses-état-action… » réalisées par l'agent. Pour les états de ces séquences, il est alors possible d'estimer kitxmlcodeinlinelatexdvpVfinkitxmlcodeinlinelatexdvp simplement par la moyenne des revenus : kitxmlcodeinlinelatexdvpV(s) = \frac{1}{N(s)} \sum Revenu(s)finkitxmlcodeinlinelatexdvp où kitxmlcodeinlinelatexdvpN(s)finkitxmlcodeinlinelatexdvp est le nombre de séquences où apparaît kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpRevenu(s)finkitxmlcodeinlinelatexdvp est le revenu après la première visite de l'état kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp, c'est-à-dire la somme pondérée des récompenses après cette visite(6).
Cette méthode de Monte-Carlo a de plus l'avantage d'estimer la valeur de chaque état indépendamment, contrairement à la programmation dynamique qui doit estimer simultanément tous les états, ce qui permet par exemple de se concentrer sur des zones de l'espace d'états plus importantes pour l'objectif du robot.
Cette méthode s'applique de la même façon pour une fonction kitxmlcodeinlinelatexdvpQ(s,a)finkitxmlcodeinlinelatexdvp, ce qui est encore plus intéressant, car pour trouver la politique optimale à partir de kitxmlcodeinlinelatexdvpV^*finkitxmlcodeinlinelatexdvp il faut disposer d'un modèle de l'environnement, ce qui n'est pas le cas en utilisant kitxmlcodeinlinelatexdvpQ^*finkitxmlcodeinlinelatexdvp. L'utilisation de kitxmlcodeinlinelatexdvpQfinkitxmlcodeinlinelatexdvp et de la méthode de Monte-Carlo permet donc de découvrir la politique optimale sans aucun modèle de l'environnement, en utilisant uniquement des expériences réalisées dans cet environnement.
III-C-3-b. Besoin d'exploration▲
La méthode de Monte-Carlo présentée doit estimer les valeurs kitxmlcodeinlinelatexdvpQ(s,a)finkitxmlcodeinlinelatexdvp à partir des récompenses obtenues après avoir réalisé l'action kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp dans l'état kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp. Ceci suppose donc que tous ces couples kitxmlcodeinlinelatexdvp(s,a)finkitxmlcodeinlinelatexdvp soient rencontrés une infinité de fois à la limite. Ceci est particulièrement problématique, car toutes les politiques ne peuvent garantir cette propriété. Il faut donc ajouter au comportement défini par la politique, un comportement d'exploration qui va assurer que toutes les actions seront réalisées avec une certaine probabilité (même faible).
Deux solutions existent pour résoudre ce problème. La première consiste à contraindre les politiques pour qu'elles associent au moins une faible probabilité proportionnelle à un paramètre kitxmlcodeinlinelatexdvp\epsilonfinkitxmlcodeinlinelatexdvp à toutes les actions. L'apprentissage converge ainsi vers la politique optimale au sein de cette classe. Cette probabilité garantit une exploration exhaustive et peut être diminuée au cours du temps lorsque les données suffisantes pour évaluer la politique ont été recueillies. Cette méthode s'appelle contrôle « on policy », car elle modifie la politique effectivement suivie par l'agent et évalue cette politique modifiée.
La seconde méthode est une méthode « off policy », car elle évalue une politique tandis que l'agent en suit une autre. Cette autre politique choisit en général l'action de la politique originale avec une probabilité kitxmlcodeinlinelatexdvp1-\epsilonfinkitxmlcodeinlinelatexdvp et une action aléatoire avec une probabilité kitxmlcodeinlinelatexdvp\epsilonfinkitxmlcodeinlinelatexdvp. Pour évaluer la politique originale, l'évaluation de Monte-Carlo utilise simplement les parties finales des séquences pour lesquelles le choix d'action correspond au choix qui aurait été fait par la politique originale, mais modifie les pondérations des récompenses pour compenser les différences de probabilité de choix des actions entre les deux politiques.
III-C-3-c. Algorithmes d'apprentissage▲
L'apprentissage utilisant une méthode de Monte-Carlo se fait en alternant l'évaluation d'une politique et son amélioration, en prenant l'action maximisant le revenu dans chaque état. Cette alternance peut se réaliser de plusieurs manières, comme pour la programmation dynamique. Soit l'évaluation est complète avant de réaliser une amélioration, soit il est possible d'alterner une évaluation utilisant une seule séquence, puis une amélioration.
III-C-4. Apprentissage par différences temporelles▲
Les deux méthodes que nous avons vues précédemment ont chacune un avantage important. La méthode de Monte-Carlo permet d'apprendre à partir d'expériences, sans aucun modèle de l'environnement. La programmation dynamique, pour sa part, possède la propriété intéressante d'utiliser les estimations des états successeurs, pour estimer la valeur d'un état ; on parle de « bootstrap ». Cette caractéristique permet une convergence beaucoup plus rapide (en termes de nombre d'exemples états/actions/récompenses) que la méthode de Monte-Carlo. Les méthodes d'apprentissage par différences temporelles vont réunir ces deux propriétés et constituent les méthodes les plus utiles en pratique en robotique.
L'évaluation de politique va donc se faire à partir d'expériences comme pour la méthode de Monte-Carlo qui utilise une moyenne pour estimer la valeur d'un état. Cette moyenne mise sous forme itérative conduit à l'équation suivante :
kitxmlcodelatexdvpV(s_t) \leftarrow V(s_t) + \alpha\left[R_t-V(s_t)\right]finkitxmlcodelatexdvpavec
kitxmlcodelatexdvpR_t = r_{t+1} +\gamma r_{t+2} + .... + \gamma^p r_{t+p+1}finkitxmlcodelatexdvpPar rapport à cette équation, l'idée est ici d'utiliser l'estimation du revenu à partir de la récompense suivante et de la valeur de l'état suivant, au lieu d'utiliser les récompenses de la suite de l'expérience. La méthode des différences temporelles utilise donc la mise à jour suivante :
kitxmlcodelatexdvpV(s_t) \leftarrow V(s_t) + \alpha\left[r_{t+1}+\gamma V(s_{t+1}) - V(s_t)\right]finkitxmlcodelatexdvpCette mise à jour se fait naturellement de manière incrémentale, au fur et à mesure des expériences de l'agent. L'équivalent de cette mise à jour pour la fonction kitxmlcodeinlinelatexdvpQfinkitxmlcodeinlinelatexdvp est donné par :
kitxmlcodelatexdvpQ(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha\left[r_{t+1}+\gamma Q(s_{t+1},a_{t+1}) - Q(s_t,a_t)\right]finkitxmlcodelatexdvpCette méthode est appelée Sarsa (pour State, Action, Reward, State, Action) et réalise une estimation « on policy » de la politique suivie, car elle utilise l'action kitxmlcodeinlinelatexdvpa_{t+1}finkitxmlcodeinlinelatexdvp qui dépend de la politique.
La méthode la plus importante de l'apprentissage par renforcement est probablement le Q-Learning, une variante « off policy » de Sarsa, qui va utiliser le maximum de la fonction sur les actions suivantes, au lieu de l'action effectivement réalisée :
kitxmlcodelatexdvpQ(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha\left[r_{t+1}+\gamma \max_a Q(s_{t+1},a) - Q(s_t,a_t)\right]\quad(7.2)finkitxmlcodelatexdvpCet algorithme fait converger kitxmlcodeinlinelatexdvpQfinkitxmlcodeinlinelatexdvp vers kitxmlcodeinlinelatexdvpQ^*finkitxmlcodeinlinelatexdvp indépendamment de la politique suivie, tant que cette politique garantit une exploration exhaustive (c.-à-.d une probabilité non nulle pour toutes les actions dans tous les états).
Comme pour les autres méthodes, la politique optimale se déduit simplement de la fonction valeur optimale.
III-C-5. Traces d'éligibilité▲
Les méthodes utilisant les différences temporelles que nous avons vues précédemment permettent de remplacer la fin d'un épisode qui serait utilisé, par une méthode de Monte-Carlo, pour estimer le revenu par la valeur estimée de l'état suivant. Or, au cours de l'apprentissage, cette valeur n'est pas forcément correcte et pourrait être remplacée par d'autres évaluations.
Le premier exemple est l'utilisation de kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp pas du futur, qui conduit à la méthode des différences temporelles à kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp pas. Dans cette méthode, le revenu est estimé par une équation de la forme :
kitxmlcodelatexdvpR_t = R_t^n = r_{t+1}+ \gamma r_{t+2} + \ldots + \gamma^n ( r_{t+n+1} + \gamma V(s_{t+n+1}) )finkitxmlcodelatexdvpLa mise à jour se ferait alors par l'équation :
kitxmlcodelatexdvpV(s_t) \leftarrow V(s_t) + \alpha\left[ R_t^n - V(s_t)\right]finkitxmlcodelatexdvpIl est également possible d'estimer kitxmlcodeinlinelatexdvpR_tfinkitxmlcodeinlinelatexdvp en utilisant des moyennes pondérées de kitxmlcodeinlinelatexdvpR_t^nfinkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvpR_t= \sum_i a_i R_t^ifinkitxmlcodelatexdvpavec kitxmlcodeinlinelatexdvp\sum a_i = 1finkitxmlcodeinlinelatexdvp
Un cas particulier intéressant de cette dernière méthode est l'utilisation d'une pondération exponentielle qui va faire décroître l'importance des expériences au fur et à mesure de leur éloignement dans le temps :
kitxmlcodelatexdvpR_t= (1-\lambda) \sum_{i=1}^\infty \lambda^i R_t^ifinkitxmlcodelatexdvpCe cas particulier est intéressant, car il peut s'appliquer simplement en utilisant les valeurs passées des récompenses, au lieu des valeurs futures (on démontre que les mises à jour sont les mêmes). On utilise pour cela une valeur auxiliaire, appelée trace d'éligibilité, que l'on définit de la manière récursive suivante :
kitxmlcodelatexdvpe_t(s)=\left\{ \begin{array}{lll} \gamma \lambda e_{t-1}(s) & si & s \neq s_t\\ \gamma \lambda e_{t-1}(s)+1 & si & s = s_t\ \end{array}\right.finkitxmlcodelatexdvp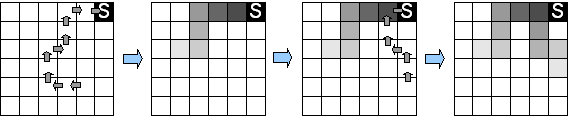
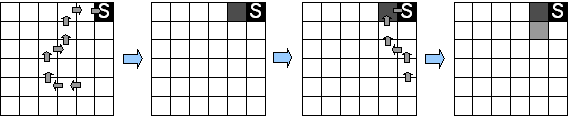
La mise à jour des valeurs se fait alors pour chaque état proportionnellement à la valeur de son éligibilité (Figure 7.5) :
kitxmlcodelatexdvpV(s_t) \leftarrow V(s_t) + \alpha e(s_t) \left[r_{t+1}+\gamma V(s_{t+1}) - V(s_t)\right]finkitxmlcodelatexdvpL'idée de cette mise à jour est de remplacer la mise à jour d'un état en utilisant des récompenses futures par la mise à jour des états passés en utilisant la récompense courante. Cela donne finalement l'algorithme TD(kitxmlcodeinlinelatexdvp\lambdafinkitxmlcodeinlinelatexdvp)(7) (algorithme 7.1). Cet algorithme se décline simplement pour les extensions Sarsa(kitxmlcodeinlinelatexdvp\lambdafinkitxmlcodeinlinelatexdvp) et Q(kitxmlcodeinlinelatexdvp\lambdafinkitxmlcodeinlinelatexdvp).
III-C-6. Application pratique▲
En robotique mobile, les espaces d'entrée et de sortie des capteurs et des effecteurs sont rarement discrets, ou, s’ils le sont, le nombre d'états est très grand. Or, l'apprentissage par renforcement tel que nous l'avons décrit utilise des espaces d'états et d'actions qui doivent être de taille raisonnable pour permettre aux algorithmes de converger en un temps utilisable en pratique.
Pour permettre d'utiliser l'apprentissage par renforcement, plusieurs approches sont possibles. La première consiste à discrétiser manuellement le problème, afin de fournir des espaces de quelques centaines d'états qui pourront être utilisés directement par des versions naïves des algorithmes (utilisant par exemple simplement des tableaux de valeurs kitxmlcodeinlinelatexdvpQ[s][a]finkitxmlcodeinlinelatexdvp, c'est cette méthode que nous avons utilisée dans l'exemple de la section suivante). Il faut cependant bien faire attention au choix des discrétisations afin qu'elles permettent un apprentissage correct en fournissant des états et des actions qui conduisent notamment à des récompenses cohérentes. Ce choix peut être relativement simple pour des capteurs intuitifs comme les capteurs de distance, mais être complexe voir impossible si l'espace d'entrée est plus abstrait ou si sa structure est peu connue (par exemple pour un jeu comme le backgammon).
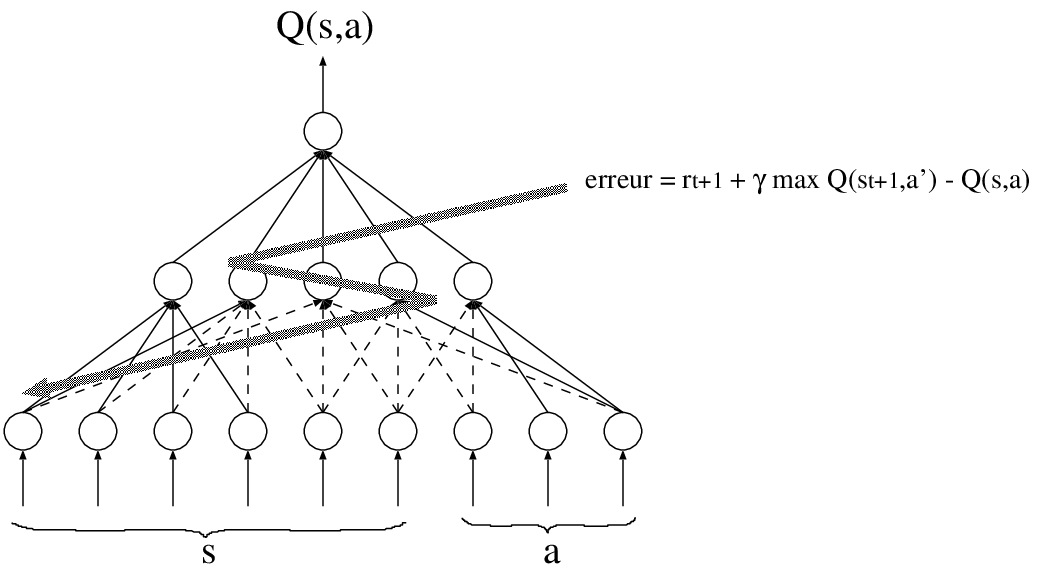
La seconde méthode va permettre de travailler directement dans les espaces d'états continus des capteurs, en utilisant des méthodes d'approximation de fonction. En effet, pour utiliser l'apprentissage par renforcement, il est simplement nécessaire d'estimer correctement la fonction kitxmlcodeinlinelatexdvpQ(s,a)finkitxmlcodeinlinelatexdvp (par exemple). Or, cette estimation peut se faire directement par un approximateur de fonction continue, par exemple un réseau de neurones (Figure 7.6), que l'on entraîne à l'aide des données recueillies sur le problème. L'utilisation de ce type d'approximation permet de travailler directement dans l'espace continu et donc de limiter les effets parasites qui pourraient apparaître suite à un mauvais choix de discrétisation. Ces méthodes peuvent posséder cependant des inconvénients, notamment de réaliser un apprentissage non local (comme dans le cas des réseaux de neurones), ce qui entraîne des modifications incontrôlées de valeurs pour des couples kitxmlcodeinlinelatexdvp(s,a)finkitxmlcodeinlinelatexdvp qui ne sont pas ceux pour lesquels on réalise l'apprentissage. Certaines méthodes utilisant d'autres types d'approximation (comme la régression pondérée localement [118]) permettent de s'affranchir de ces contraintes.
III-C-7. Exemple de mise en œuvre▲
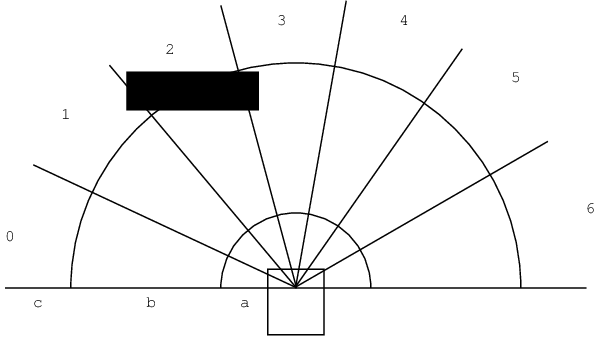
Dans cet exemple, nous avons utilisé un algorithme de Q-Learning très simple pour apprendre à un robot à éviter les obstacles. Le robot possède un télémètre laser et une base mobile différentielle. Nous avons discrétisé les données du télémètre selon le schéma de la Figure 7.7 pour constituer un espace d'entrée de 2187 états. Les actions ont été discrétisées en trois actions élémentaires : avancer, tourner à droite, tourner à gauche.
|
Figure 7.7 - Discrétisation de l'espace d'états : pour chaque secteur, de 0 à 6, une valeur kitxmlcodeinlinelatexdvpO_ifinkitxmlcodeinlinelatexdvp est calculée en fonction de la présence ou de l'absence d'obstacles dans les zones a, b et c : 0 si un obstacle est dans a, 1 si un obstacle est dans b et 2 sinon. L'état kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp est la valeur en base 3 fournie par les des kitxmlcodeinlinelatexdvpO_ifinkitxmlcodeinlinelatexdvp : kitxmlcodeinlinelatexdvp\sum_k 3^k O_kfinkitxmlcodeinlinelatexdvp. Dans l'exemple, kitxmlcodeinlinelatexdvpO_0=2, O_1=2, O_2=1, O_3=1, O_4=2, O_5=2, O_6=2finkitxmlcodeinlinelatexdvp et donc kitxmlcodeinlinelatexdvps = 2150finkitxmlcodeinlinelatexdvp. |
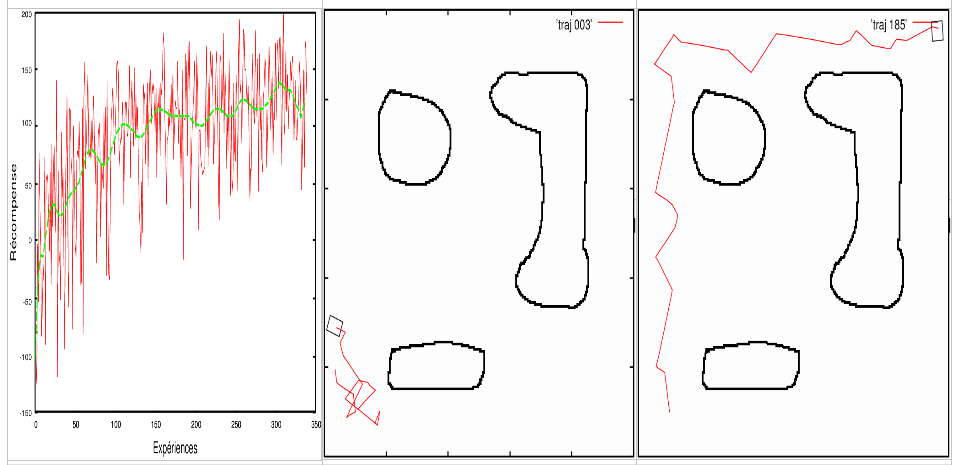
La récompense était de -10 lorsque le robot percutait un obstacle (il est alors remis à son point de départ) et +3 lorsque le robot choisissait l'action d'avancer. L'algorithme de Q-Learning utilise un simple tableau de 2187x3 cases pour représenter la fonction kitxmlcodeinlinelatexdvpQfinkitxmlcodeinlinelatexdvp. La courbe 7.8 donne l'évolution au cours du temps des récompenses obtenues sur des épisodes de 100 pas de temps. Les pas de temps ont une longueur variable et correspondent aux changements d'état. Un épisode dure en moyenne 35 secondes. La figure illustre également les trajectoires aléatoires initiales et le résultat après convergence de l'algorithme.
III-C-8. Pour aller plus loin▲
Reinforcement Learning : An Introduction de Richard S. Sutton and Andrew G. Barto. MIT Press, Cambridge, MA, 1998. A Bradford Book. Disponible en ligne(8)
Le reinforcement learning repository : http://www-anw.cs.umass.edu/rlr/