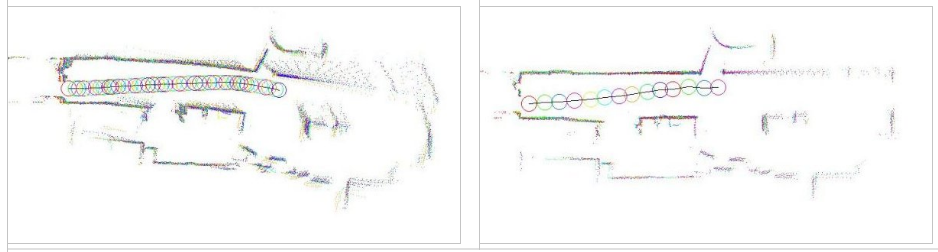IV. Navigation utilisant une carte▲
Cette partie présente les méthodes de navigation basées sur des cartes qui permettent à un robot de prendre en compte des buts à long terme en utilisant des informations mémorisées sur la structure de son environnement. Ces méthodes se basent sur trois processus : la cartographie, la localisation et la planification, détaillés dans les différents chapitres.
IV-A. Localisation, cartographie et planification▲
IV-A-1. Trois problèmes de la navigation par carte▲
Le processus complet qui permet à un robot de mémoriser son environnement, puis de s'y déplacer pour rejoindre un but, peut être découpé en trois phases : la cartographie, la localisation et la planification. Ces trois phases permettent de répondre aux trois questions fondamentales pour la tâche de navigation [93] : Où suis-je ? Où sont les autres lieux par rapport à moi ? Comment puis-je atteindre mon but ?
- La cartographie est la phase qui permet la construction d'une carte reflétant la structure spatiale de l'environnement à partir des différentes informations recueillies par le robot.
- Une telle carte étant disponible, la localisation permet alors de déterminer la position du robot dans la carte qui correspond à sa position dans son environnement réel.
- La planification, enfin, est la phase qui permet, connaissant la carte de l'environnement et la position actuelle du robot, de décider des mouvements à effectuer afin de rejoindre un but fixé dans l'environnement.
Ces trois phases sont évidemment fortement interdépendantes. L'ordre dans lequel elles sont citées fait directement apparaître le fait que la seconde phase dépend de la première. En effet, estimer sa position au sein d'une carte de l'environnement suppose implicitement que cette carte existe et qu'elle contient la position courante du robot. De même, la troisième phase dépend des deux premières, car la planification suppose que l'on connaisse sa position et que la carte de l'environnement représente une portion de l'environnement contenant au moins un chemin reliant cette position au but qui doit être atteint.
Mais la relation entre les deux premières phases est plus subtile qu'une simple relation d'antériorité : c'est le même problème que pour l'œuf et la poule. Chacun des deux éléments peut, en effet, être considéré comme préalable à l'autre, mais dépend aussi de l'autre pour sa réalisation. Dans le cas de la cartographie et de la localisation, nous avons déjà vu que la localisation repose sur une phase préalable de cartographie. Mais pour construire une carte, il est nécessaire de savoir où ajouter, dans la carte partielle déjà existante, toute nouvelle information recueillie par le robot. Cela requiert donc une phase préalable de localisation au sein de la carte partielle déjà existante. Pour un robot complètement autonome, il est donc impossible de ne pas traiter ces deux problèmes simultanément. Dans la littérature scientifique, on parle ainsi de problème de « Simultaneous Localization and Mapping » (SLAM).
Dans le cas où l'on autorise un opérateur humain à intervenir dans le processus, il est évidemment possible de découpler ces deux phases. Dans les applications réelles, il est fréquent que l'on fournisse au robot une carte construite au préalable et qu'on ne s'intéresse qu'à l'estimation de la position au sein de cette carte pour qu'il puisse accomplir sa tâche. La carte peut alors être obtenue de différentes manières. Il est par exemple possible d'utiliser un plan d'architecte d'un bâtiment pour le transformer en une carte utilisable par le robot. Il est également possible d'utiliser le robot dans une phase supervisée de cartographie. Au cours de cette phase, la position du robot peut être calculée de manière précise par un dispositif externe au système de navigation, et ne nécessite donc pas que le système estime de lui-même la position. Connaissant la position précise du robot, il est alors relativement simple de construire une carte de l'environnement. Il est également possible d'utiliser un algorithme de SLAM comme sur un robot autonome, mais de corriger la carte avant de l'utiliser réellement. Cela permet notamment d'ajouter des obstacles « virtuels » pour interdire certains passages tels que les escaliers.
IV-A-2. Quelques hypothèses de travail▲
IV-A-2-a. Estimation de la position et de la direction▲
À ce stade, il convient de préciser la notion de position que nous emploierons. En effet, la position d'un robot est définie à la fois par son emplacement spatial, estimé par rapport à un point de référence et par sa direction, estimée par rapport à une direction de référence. Ces deux quantités sont couplées, mais ont des statuts qui peuvent être distincts en pratique.
Lors du mouvement, la direction du robot influence la manière dont varie sa position, mais peut parfois être contrôlée indépendamment. Dans le cas de plates-formes holonomes, ce découplage permet notamment de simplifier le processus de planification en ne tenant pas compte de la direction du robot, laquelle peut être contrôlée sans influencer la position. La variable importante est alors la position du robot, la direction devant être estimée pour pouvoir agir, mais non pour planifier.
Cette indépendance relative au niveau de la planification peut conduire à des systèmes d'estimation de la position et de la direction séparés. Cette séparation est supportée par le fait que la direction d'un robot peut être mesurée par des capteurs indépendamment de l'estimation de sa position. Il est par exemple possible d'utiliser une boussole qui mesure la direction par rapport à la direction du pôle magnétique, ou un gyroscope qui mesure la direction par rapport à une direction arbitraire fixe.
Le choix de représenter et d'estimer de manière séparée la position et la direction n'interdit toutefois pas des interactions entre ces informations. L'estimation de la position utilisera évidemment celle de la direction pour pouvoir intégrer de nouvelles données lors du mouvement du robot. L'estimation de la direction pourra également dépendre de la position par un système de recalage qui utilisera la perception d'un point de référence connu depuis une position connue pour estimer la direction.
Ceci dit, la majorité des systèmes métriques (voir section III.B.2Cartes métriques) vont néanmoins estimer la position et la direction ensemble, soit en 2D (trois degrés de liberté), soit en 3D (six DDL).
IV-A-2-b. Environnements statiques et dynamiques▲
Il convient également de préciser les types d'environnements que nous considérons ici. En effet, les robots sont amenés à se déplacer dans une grande variété d'environnements qui peuvent être regroupés en deux grandes catégories : les environnements statiques et les environnements dynamiques. Les environnements statiques sont des environnements qui ne subissent pas de modification au cours du temps. Cette stabilité concerne à la fois leur structure spatiale et leur apparence pour les capteurs du robot. Cela exclut la majorité des environnements dans lesquels les humains évoluent quotidiennement. Les environnements dynamiques, pour leur part, présentent des caractéristiques qui évoluent au cours du temps. La plupart des environnements courants appartiennent évidemment à la seconde catégorie. Par exemple, un environnement de bureau est dynamique, du fait des personnes qui y travaillent, des chaises qui y sont déplacées ou des portes qui y sont ouvertes ou fermées.
Il est, de plus, possible de distinguer deux catégories d'éléments dynamiques. La première catégorie regroupe les éléments variables qui ne caractérisent pas l'environnement. De tels éléments peuvent être considérés comme du bruit qui n'a pas d'intérêt dans la modélisation de l'environnement pour la planification. C'est, par exemple, le cas des personnes évoluant dans un bureau, ou des chaises déplacées. Ces environnements peuvent être considérés comme constitués d'une partie statique sur laquelle se superposent différentes sources de bruit. La partie statique est la partie la plus importante à modéliser pour parvenir à une navigation efficace. Deux effets du bruit doivent toutefois être pris en compte. Il faut premièrement veiller à ce qu'il n'empêche pas la réalisation de commandes issues de la planification. Cela est en général réalisé par le système de contrôle (dans le cadre d'une architecture hybride, voir section I.A.2.cContrôleurs hybrides), séparé du système de navigation, qui réalise l'interface avec la partie physique du robot. De plus, il faut prendre en compte ce bruit au niveau de la cartographie et de la localisation afin qu'il ne nuise pas à la modélisation de la seule partie statique de l'environnement et ne conduise pas à une mauvaise estimation de la position. Les méthodes de navigation actuelles (présentées dans ce cours) sont plus ou moins robustes face à ces bruits, mais cette robustesse reste généralement limitée, surtout pour la partie cartographie. Il commence cependant à apparaître des méthodes prenant explicitement en compte ces éléments dynamiques, qui permettent d'envisager d'utiliser des robots dans des environnements assez fortement bruités (par exemple [143]).
La seconde catégorie d'éléments dynamiques regroupe les éléments variables qui caractérisent l'environnement et peuvent avoir un intérêt pour la planification. C'est, par exemple, le cas des portes qui modifient la structure spatiale de l'environnement et peuvent entraîner des modifications de trajectoires en fonction de leur état. Ils doivent donc être enregistrés dans la carte si l'on veut pouvoir les prendre en compte.
La plupart des systèmes de navigation robotiques s'intéressent aux environnements appartenant à l'une des deux premières catégories. Les environnements sont donc supposés être soit statiques, soit entachés d'un bruit qui n'influence pas la planification. Ces systèmes s'intéressent donc à modéliser la partie statique des environnements qui va être utile pour la localisation et la planification. Il faut toutefois noter que ces systèmes, qui ne modélisent pas les éléments dynamiques de la seconde catégorie, sont néanmoins capables d'évoluer dans des environnements qui contiennent de tels éléments. Pour ce faire, ces systèmes sont en général capables de vérifier que la trajectoire planifiée est correctement exécutée. En cas de problème d'exécution, un chemin alternatif ne passant pas par la zone qui ne peut être atteinte est alors recherché. Cette méthode, qui ne modélise pas explicitement les portes, par exemple, est néanmoins capable de provoquer des détours si une porte fermée bloque un chemin.
IV-B. Représentations de l'environnement▲
Les deux utilisations possibles des perceptions présentées dans le chapitre I.BSources d'information (avec et sans modèle métrique) trouvent un parallèle dans deux types de représentations de l'environnement.
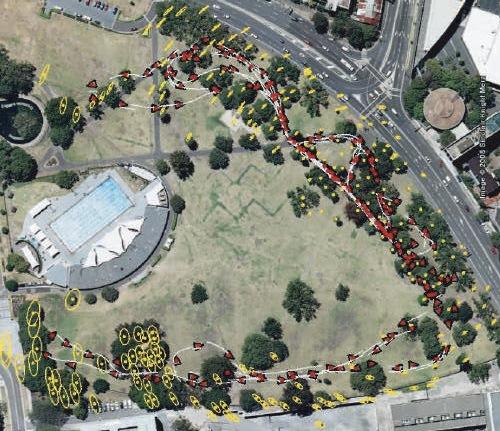
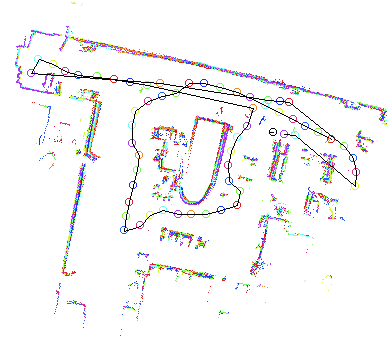
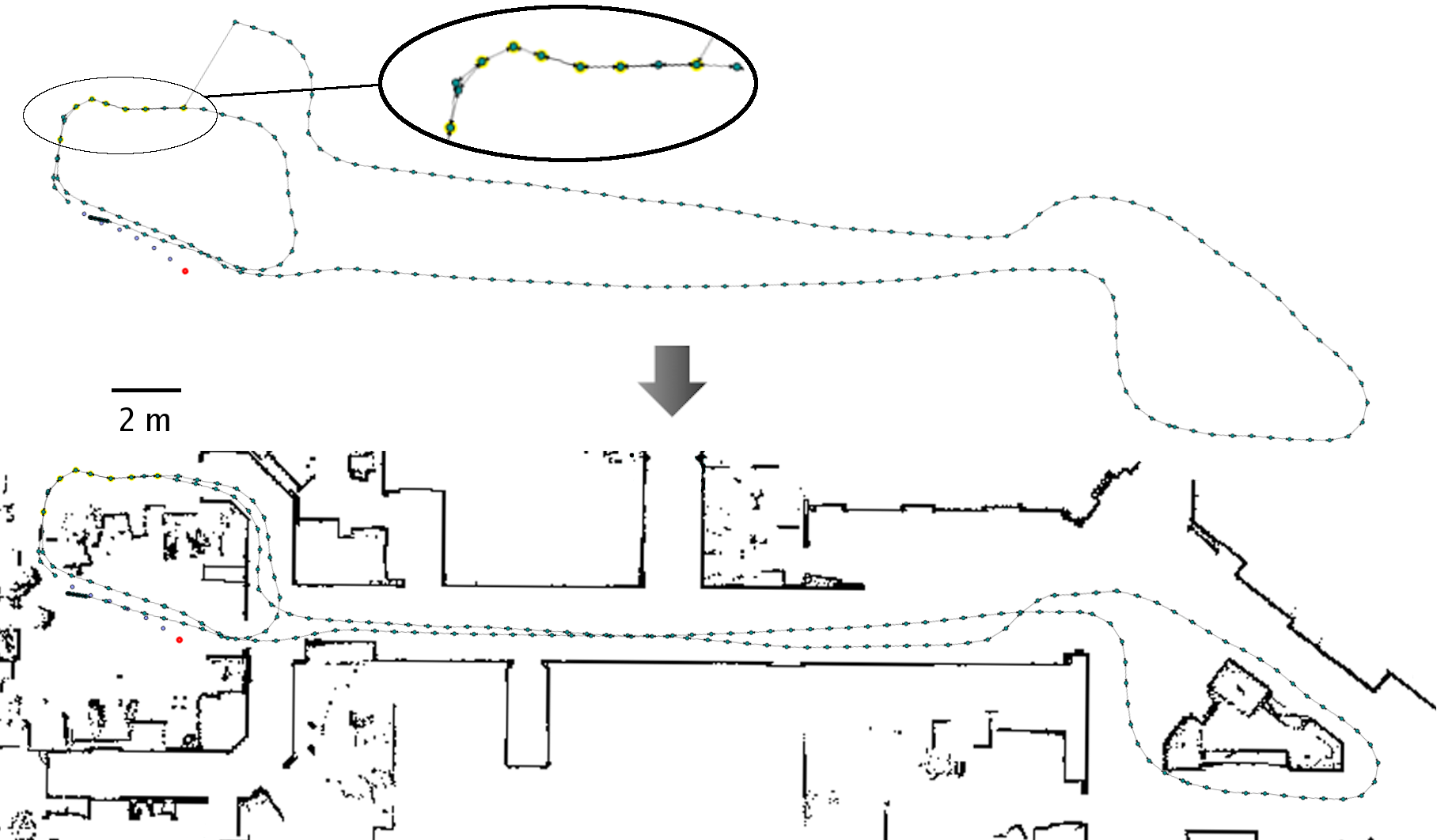
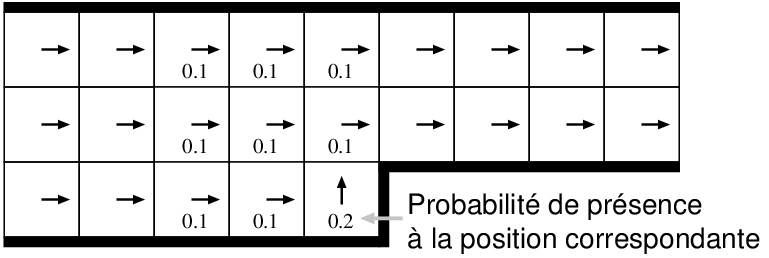
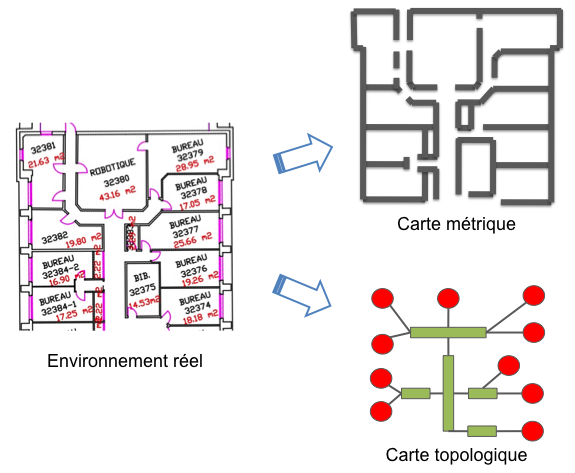
Lorsqu’ aucun modèle métrique n'est utilisé pour les capteurs, les données sont en général mémorisées dans une carte topologique [82, 131] (cf. Figure 9.1). Dans une telle carte, un ensemble de lieux et leurs relations de voisinage sont mémorisés. Chaque lieu est défini au moyen de perceptions recueillies lorsque le robot se trouve à la position correspondante. Les relations entre lieux sont en général déduites des données proprioceptives.
En revanche, lorsqu'un modèle métrique des capteurs est utilisé, les données peuvent être mémorisées au sein d'une carte métrique [101, 29] (cf. Figure 9.1) qui rassemble dans un même cadre de référence les données proprioceptives et les perceptions. La carte contient alors un ensemble d'objets, ayant chacun une position associée. Naturellement, il est possible de construire une carte topologique lorsqu'un modèle métrique est utilisé. Dans ce cas, toutefois, les perceptions ne sont en général pas utilisées pour estimer la position relative des lieux visités, mais seulement pour caractériser ces lieux.
Il est également possible d'utiliser des représentations hybrides qui vont avoir des caractéristiques à la fois topologiques et métriques afin de bénéficier des avantages de chacune des approches.
Notons que la notion de topologique et de métrique est différente de celle mentionnée pour les stratégies de navigation dans l'introduction. Ici, cette notion fait référence à la manière dont les informations sont mémorisées et non à la stratégie de navigation utilisée. Ainsi une carte topologique pourra contenir des informations métriques et pourra être utilisée pour une stratégie de navigation métrique, au sens donné dans l'introduction. Dans la suite de ce cours, le concept topologique/métrique fera toujours référence au type de carte utilisé, et non à la stratégie correspondante.
IV-B-1. Cartes topologiques▲
IV-B-1-a. Description▲
Les cartes topologiques permettent de représenter l'environnement du robot sous forme de graphe. Les nœuds du graphe correspondent à des lieux, c'est-à-dire des positions que le robot peut atteindre. Les arêtes liant les nœuds marquent la possibilité pour le robot de passer directement d'un lieu à un autre et mémorisent en général la manière de réaliser ce passage.
La détection et la mémorisation des lieux reposent en général sur deux procédures qui utilisent les perceptions. La première permet simplement de comparer deux perceptions et donc de reconnaître un lieu de la carte ou de détecter un lieu nouveau. La seconde procédure permet de mémoriser un nouveau lieu ou d'adapter la définition d'un lieu lors des passages successifs du robot en ce lieu. Comme nous l'avons déjà mentionné, la reconnaissance d'un lieu est soumise aux problèmes de la variabilité perceptuelle et du perceptual aliasing. En conséquence, la première procédure peut donner des résultats erronés. Par exemple, un lieu déjà visité peut ne pas être reconnu, ou un lieu nouveau peut être confondu avec un lieu déjà mémorisé. Pour résoudre ces problèmes, la reconnaissance des lieux fera donc appel aux données proprioceptives en plus des perceptions. De nombreuses méthodes, dont les plus importantes seront décrites dans la suite du cours, ont été mises en œuvre dans ce but.
Les données mémorisées dans les arêtes du graphe sur les relations de voisinage entre lieux proviennent, pour leur part (en général), des données proprioceptives. Cela est caractéristique des cartes topologiques, dans lesquelles les perceptions ne sont en général pas utilisées pour estimer les positions relatives des lieux visités, mais seulement pour reconnaître un lieu. Ces données peuvent être des informations sur les positions relatives des nœuds, ou des informations sur les actions à effectuer pour parcourir cette arête.
IV-B-1-b. Avantages▲
Un avantage important des cartes topologiques est qu'elles ne requièrent pas de modèle métrique des capteurs pour fusionner les données proprioceptives et les perceptions au sein d'une représentation unifiée de l'environnement. Cela est avantageux pour deux raisons. D'une part, ces modèles métriques peuvent, comme nous l'avons vu, être difficiles à obtenir ou s'avérer peu fiables. Se passer de modèle métrique permet par exemple d'utiliser simplement des images panoramiques pour la reconnaissance de lieux. D'autre part, le fait de ne pas fusionner les deux sources d'informations permet de séparer les influences des erreurs correspondantes. En effet, l'estimation de la position d'objets, lorsque l'on utilise un modèle métrique, dépend à la fois des valeurs mesurées par les capteurs et de la position du robot. Une erreur sur la position d'un objet peut donc provenir des deux sources. Déterminer la contribution de chacune des sources peut être difficile. Dans les cartes topologiques, au contraire, le bruit sur les mesures des capteurs influe principalement sur la reconnaissance des lieux, tandis que le bruit sur les données proprioceptives influe principalement sur la position associée à chaque lieu.
La mémorisation de l'environnement sous forme d'un ensemble de lieux distincts autorise en général une définition des lieux plus directement reliée aux capacités perceptives du robot. En effet, comme les perceptions ne sont pas transformées dans un repère métrique, il n'y a pas de limitation au type de capteurs utilisables (cf. la section I.B.2Informations extéroceptives). Cette utilisation directe des perceptions permet un meilleur ancrage dans l'environnement, c'est-à-dire une meilleure mise en relation du robot avec son environnement. Puisque la carte est très proche des données brutes perçues par le robot, il est en général assez simple de comparer et de mémoriser des lieux de l'environnement.
Cette proximité avec les données brutes conduit en général la représentation topologique à utiliser beaucoup moins de concepts de haut niveau que les représentations métriques. La carte topologique reste ainsi proche des possibilités du robot, en mémorisant ses perceptions et ses déplacements possibles, indépendamment de concepts de plus haut niveau tels que des objets ou des obstacles.
La discrétisation de l'environnement correspondant au choix des lieux représentés dans la carte est un autre point fort des cartes topologiques. Cette discrétisation est en effet très utile pour la planification des mouvements du robot, qui se réduit alors à la recherche de chemin dans un graphe. Cette recherche est, en termes de complexité algorithmique, beaucoup plus simple que la recherche d'un chemin dans un espace continu à deux dimensions. Cet avantage est encore plus important lorsque les lieux représentés dans la carte correspondent à des structures humaines telles que les portes, les couloirs ou les pièces. La discrétisation permet alors de décrire et de résoudre les problèmes de manière naturelle pour les humains, par exemple en donnant l'ordre d'aller au bureau B744, plutôt que de dire d'aller à la position définie par les coordonnées x=354,y=285.
IV-B-1-c. Inconvénients▲
Comme nous l'avons déjà mentionné, l'utilisation directe des perceptions sans modèle métrique empêche d'estimer ces données pour des positions non visitées. En conséquence, les cartes topologiques nécessitent en général une exploration très complète de l'environnement pour le représenter avec précision. En particulier, tous les lieux intéressants que l'on souhaite trouver dans la carte devront être visités au moins une fois au cours de la construction de la carte, parce qu'ils ne peuvent pas être perçus à distance. Dans le cas où les lieux représentés sont des structures d'assez haut niveau (comme des couloirs ou des pièces), cela n'est pas gênant, car ces lieux sont peu nombreux et une exploration exhaustive est donc relativement rapide. En revanche, dans les cartes topologiques représentant des lieux avec une assez grande densité spatiale, cela peut être un inconvénient, car l'exploration complète de l'environnement demandera un temps important.
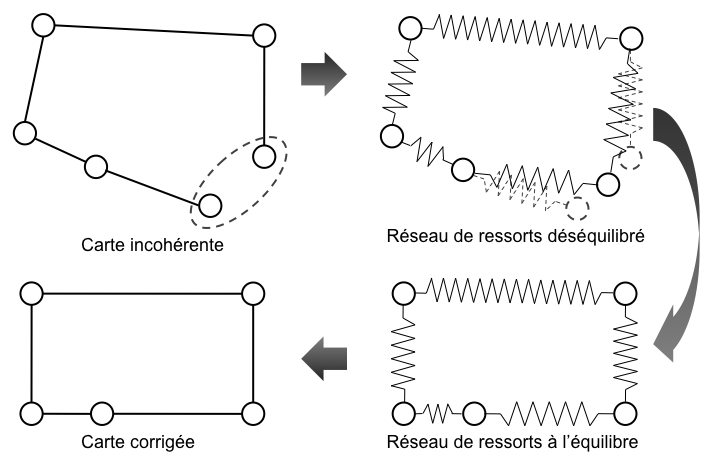
La reconnaissance des lieux de l'environnement peut également être difficile dans le cas de capteurs très bruités, ou d'environnements très dynamiques. Elle est, de plus, très sensible au problème de perceptual aliasing. Ces difficultés conduisent à des problèmes de fausse reconnaissance, c'est-à-dire à la reconnaissance d'un lieu donné alors que le robot se trouve dans un autre lieu. À leur tour, ces fausses reconnaissances conduisent à une mauvaise topologie de la carte et à des liens qui relient des nœuds de la carte qui ne sont pas physiquement reliés dans l'environnement. Ces difficultés rendent problématique la construction de cartes topologiques dans des environnements de grande taille, car la carte résultante risque d'être incohérente. Il devient alors très difficile d'estimer correctement la position du robot au sein de cette carte et de lui ajouter de nouvelles informations sans erreurs.
Comme nous l'avons vu, la représentation de l'environnement peut être assez proche des données brutes des capteurs du robot, ce qui peut être un avantage du point de vue de l'autonomie du robot. Toutefois, cette représentation centrée sur l'individu peut poser des problèmes pour la réutilisation de la carte. En effet, le manque de représentation de l'environnement indépendante de l'individu et l'absence de modèle métrique des capteurs ne permettront pas d'adapter la carte à un robot avec des capteurs légèrement différents. En effet, si l'on dispose d'un tel modèle, l'adaptation se fait simplement au niveau du modèle de capteur, sans modification de la carte elle-même. Cela est plus difficile avec une carte topologique, au sein de laquelle il est quasiment impossible de changer les données recueillies par un capteur pour les transformer en données telles qu'un autre capteur aurait pu les acquérir. De plus, cette représentation centrée sur un individu est moins naturelle pour un opérateur humain, plus habitué aux représentations objectives du type plan d'architecte, ce qui peut être gênant lorsque l'on souhaite une interaction forte entre un opérateur et le robot.
IV-B-1-d. Mise en œuvre▲
IV-B-1-d-i. Définition des nœuds▲
Le choix de ce que vont représenter les nœuds de la carte détermine tout le processus de construction de la carte topologique. Ce choix est lié aux capacités de perception dont on a doté le robot, lequel devra être capable de détecter les lieux en question. La localisation et la mise à jour de la carte se feront chaque fois qu'un tel lieu aura été détecté. La détection de ces lieux peut être contrainte par les choix d'un opérateur humain ou être complètement autonome.
Nœuds définis par le concepteur
La première possibilité est de définir directement quels lieux doivent être détectés par le robot et comment ils doivent l'être. Des procédures sont alors écrites qui permettent de détecter spécifiquement chaque type de lieu. Le choix le plus courant est l'utilisation de couloirs, de portes et d'intersections [33, 69, 83, 125]. Lorsque ce choix est fait, un très petit nombre de lieux différents peuvent être détectés, ce qui rend le problème du perceptual aliasing omniprésent. Les systèmes concernés dépendent donc en général fortement des données proprioceptives pour parvenir à utiliser ces représentations.
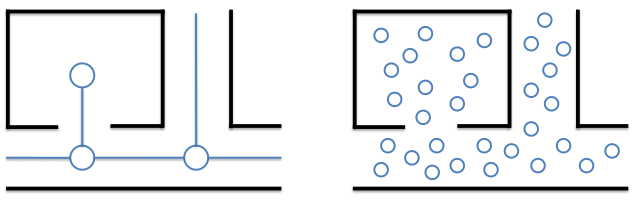
Nœuds définis à des positions canoniques
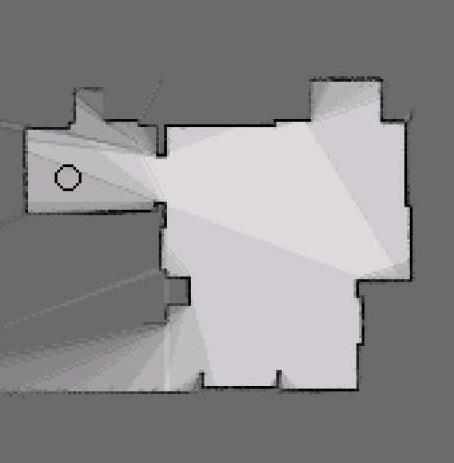
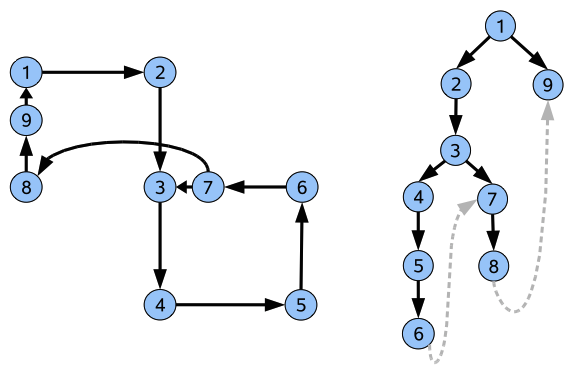
Plutôt que de définir complètement les lieux que peut détecter le robot, le concepteur peut simplement définir dans quels types de situations le robot peut enregistrer un lieu, laissant le soin de définir chaque lieu précisément au moment de la découverte du lieu (Figure 9.2, à gauche). Par exemple, le concepteur peut doter le robot de la capacité générale de détecter des portes. Lorsque le robot détectera une porte, il enregistrera un nouveau nœud dans la carte, mais ce nœud sera défini par la situation précise dans laquelle il se trouve quand il rencontre cette porte. Il pourra, par exemple, enregistrer la couleur de la porte, le numéro qui est inscrit dessus ou une image de l'environnement vu depuis cette position. Cette méthode de définition des nœuds a été proposée par Kuipers et Byun [82] sous le nom de distinctive places, puis utilisée sous une forme différente par Engelson et McDermott [43] et par Kortenkamp et Weymouth [80] sous le nom de gateways.
Nœuds définis de manière non supervisée
La troisième méthode pour définir les nœuds d'une carte topologique consiste à les définir comme des zones où les perceptions sont approximativement constantes (Figure 9.2, à droite). Cela est obtenu en général par la catégorisation non supervisée des perceptions [9, 36, 51, 54, 84, 93, 98, 105, 141, 142]. Ces perceptions sont donc regroupées en catégories contenant des données similaires, sans que ces catégories soient spécifiées par un concepteur humain. Chaque catégorie correspond alors à un ou plusieurs nœuds de la carte. Le nœud correspondant à une catégorie étant unique dans le cas où il n'y a pas de perceptual aliasing. Cette méthode est bien adaptée à des robots autonomes, car la catégorisation ne nécessite aucun superviseur ni aucune définition a priori des données correspondant à un nœud. À ce titre, elle est utilisée dans tous les systèmes de navigation qui s'inspirent des comportements de navigation des animaux [6, 12, 25, 124, 137].
Pour mettre en œuvre une telle approche, il faut définir un critère qui permette de décider quand un nouveau lieu a été atteint. Le choix le plus évident est de comparer constamment la situation courante à celle du précédent nœud reconnu. Lorsque la différence est suffisamment importante, on considère qu'un nouveau lieu a été atteint. Cette méthode est utilisée par certains modèles [51, 54, 84, 98, 105], mais requiert que les perceptions soient comparées en temps réel, ce qui peut être difficile pour certains capteurs (les caméras, par exemple). D'autres modèles considèrent donc plus simplement qu'un nouveau nœud a été atteint lorsque la distance parcourue depuis la dernière reconnaissance est assez grande [6, 137, 142, 145].
IV-B-1-d-ii. Définition des arêtes▲
Les arêtes reliant les nœuds permettent de mémoriser des données sur les relations de voisinage entre lieux représentés par les nœuds. Ces données sont en général obtenues grâce aux informations proprioceptives. Elles peuvent être plus ou moins précises et représentées sous diverses formes.
Relation d'adjacence
La première information que porte une arête est une information d'adjacence entre les deux lieux représentés par les nœuds qu'elle connecte. Cette relation peut être bidirectionnelle ou non. L'existence d'une arête signifie donc que le robot peut passer directement d'un lieu à l'autre, sans passer par un lieu intermédiaire. Si certains modèles ne mémorisent que cette information d'adjacence [51, 55, 69, 79, 106, 141], cette information est prise en compte dans tous les modèles, même si des informations supplémentaires sont enregistrées dans les arêtes.
Relations métriques
Des informations métriques sur la position relative des lieux peuvent être mémorisées dans les arêtes. Ces informations portent en général sur la position relative des lieux reliés par l'arête [43, 66, 82, 83, 105, 125, 127, 142] (Figure 9.2, à gauche). Elles sont fournies et quantifiées par les données proprioceptives lorsque le robot se déplace d'un lieu à l'autre. Cette méthode présente l'avantage de limiter l'accumulation de l'erreur des données proprioceptives, puisque ces données ne sont utilisées que sur la distance reliant un nœud à un autre. Cette distance est en général assez courte pour éviter une accumulation d'erreurs trop importante. Les cartes topologiques utilisant de telles informations métriques sont appelées par certains auteurs cartes diktiométriques [43], ou carte topométriques [13].
Association de positions aux nœuds
Dans le but d'intégrer les données proprioceptives à une carte topologique, il est également possible d'associer une position à chacun des nœuds (Figure 9.2, à droite). Cette position se mesure dans l'espace dans lequel s'expriment les données proprioceptives et correspond à la position des différents lieux dans l'environnement. Ce type de carte se rapproche fortement des cartes métriques, à la différence que seuls les lieux visités par le robot, et non les objets perçus par le robot, sont mémorisés. L'inconvénient, par rapport à l'approche précédente, est qu'il est nécessaire de corriger les informations proprioceptives, car elles ne sont plus utilisées localement. Chaque nœud ayant une position dans un cadre de référence global, il est possible de se contenter de cette information, sans ajouter de liens entre les nœuds [108, 6, 12]. Toutefois, certains modèles utilisent également des liens pour mémoriser l'information d'adjacence [98, 137, 84, 146, 36, 142, 33]. Comme l'information de position de chaque nœud est absolue, ce type de carte peut être appelé carte diktiométrique absolue.
Relation implicite
Dans certains cas, il est possible de retrouver les relations de position entre les lieux au vu des seules perceptions qui les représentent. Cela est possible, par exemple, lorsque les lieux sont définis par la configuration d'amers distants qui peuvent être perçus par le robot lorsqu'il se trouve à cette position. Un certain nombre d'amers communs, visibles depuis deux lieux différents permettront d'avoir des informations sur la position relative de ces lieux. L'existence d'amers communs peut donc être utilisée comme lien implicite [93, 124, 25].
IV-B-2. Cartes métriques▲
IV-B-2-a. Description▲
Dans une carte métrique, l'environnement est représenté par un ensemble d'objets auxquels sont associées des positions dans un espace métrique, généralement en deux dimensions. Cet espace est, la plupart du temps, celui dans lequel s'exprime la position du robot estimée par les données proprioceptives. Les perceptions permettent, en utilisant un modèle métrique des capteurs, de détecter ces objets et d'estimer leur position par rapport au robot. La position de ces objets dans l'environnement est alors calculée en utilisant la position estimée du robot. La fusion des deux sources d'informations au sein d'un même cadre de représentation est caractéristique des cartes métriques.
Les objets mémorisés dans la carte peuvent être très divers et seront détaillés dans la suite de cette section. Dans certaines implantations, ces objets correspondent aux obstacles que le robot pourra rencontrer dans son environnement. La carte de l'environnement correspond alors directement à l'espace libre, c'est-à-dire à l'espace dans lequel le robot peut se déplacer.
IV-B-2-b. Avantages▲
L'avantage principal des cartes métriques est de permettre de représenter l'ensemble de l'environnement, et non un petit sous-ensemble de lieux comme le font les cartes topologiques. Cette représentation complète permet ainsi d'estimer avec précision et de manière continue la position du robot sur l'ensemble de son environnement. De plus, cette représentation complète ne se limite pas aux positions physiquement explorées, mais s'étend à toutes les zones que le robot a pu percevoir depuis les lieux qu'il a visités. Cette propriété peut permettre la construction d'une carte plus exhaustive de l'environnement en un temps plus court.
Un autre avantage des cartes métriques est lié au fait que la position du robot est définie de manière non ambiguë par ses coordonnées au sein de l'espace dans lequel la carte est représentée. Il s'ensuit une utilisation simple et directe de toutes les informations métriques fournies par les données proprioceptives ou les perceptions. Cela est un avantage par rapport aux cartes topologiques où les positions possibles du robot sont limitées aux nœuds présents dans la carte et sont donc relativement imprécises. Une telle représentation, dans laquelle chaque nœud peut couvrir une zone étendue de l'environnement, rend plus difficile l'utilisation des données métriques, car la position relative de deux zones est moins bien définie.
La représentation de l'environnement indépendante de l'individu utilisée dans les cartes métriques apporte un certain nombre d'avantages supplémentaires. Comme nous l'avons mentionné à propos des cartes topologiques, une telle représentation permet une réutilisation plus facile d'une carte sur des robots différents, équipés de capteurs différents, l'essentiel de l'adaptation se déroulant au niveau des modèles métriques des capteurs. Ce type de représentation est aussi facilement interprétable par un humain, ce qui peut être important dans le cas où il doit intervenir dans les déplacements du robot.
Cette représentation peut de plus utiliser des concepts de plus haut niveau, tels que des objets, des obstacles ou des murs. Cela permet un apport de connaissance plus facile de la part des humains, par exemple pour imposer que les murs détectés soient perpendiculaires ou parallèles.
IV-B-2-c. Inconvénients▲
Lors de l'utilisation de cartes métriques, les données proprioceptives ont en général une importance supérieure à celle qu'elles ont dans l'utilisation d'une carte topologique. Par conséquent, une odométrie plus fiable peut être requise. Le niveau de fiabilité nécessaire peut être atteint en imposant des limitations sur l'environnement du robot. Par exemple, il est possible d'imposer que tous les couloirs soient orthogonaux, afin de pouvoir corriger efficacement la dérive de l'estimation de la position.
Comme nous l'avons mentionné dans la section I.B.2Informations extéroceptives, un modèle métrique des capteurs peut être difficile à obtenir. Les problèmes liés au bruit des capteurs et à la difficulté de modéliser de manière fiable leur relation avec l'environnement constituent donc un point faible des cartes métriques.
Enfin, le calcul de chemin au sein des cartes métriques peut être plus complexe, car la planification se déroule dans un espace continu et non dans un espace préalablement discrétisé, comme c'est le cas pour les cartes topologiques. De nombreuses méthodes recourent d'ailleurs à l'extraction d'une carte topologique depuis la carte métrique pour réaliser cette opération de planification [87].
IV-B-2-d. Mise en œuvre▲
Deux méthodes principales sont utilisées pour mémoriser des informations sous forme de carte métrique. La première méthode consiste à extraire explicitement des objets des perceptions et à les enregistrer dans la carte avec leur position estimée. Les objets peuvent être de types très variés et se situer à différents niveaux d'abstraction. La seconde méthode s'attache à représenter directement l'espace libre accessible au robot et les zones d'obstacles qu'il ne peut pas franchir, sans avoir recours à l'identification d'objets individuels.
IV-B-2-d-i. Représentation d'objets▲
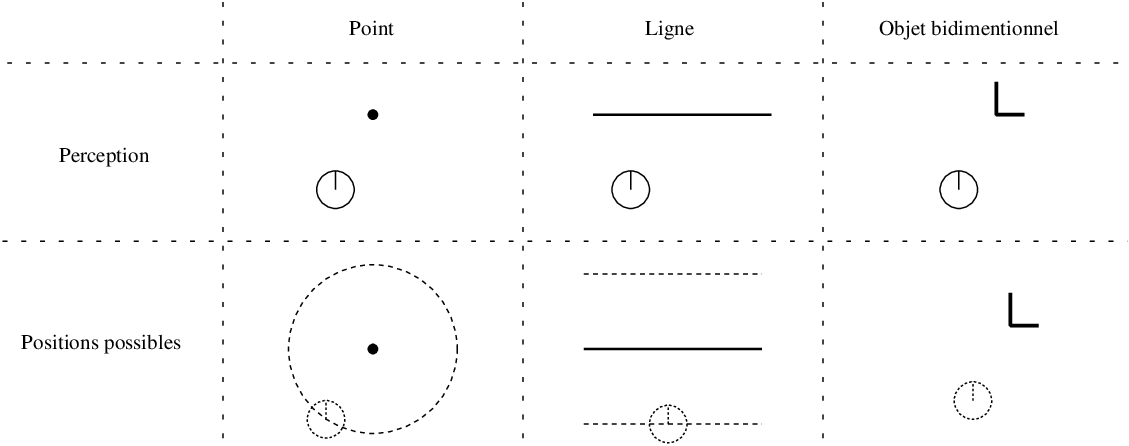
Points
Les objets les plus simples qui peuvent être utilisés sont des points [93, 111, 44] que l'on appelle dans ce cas amers (terme de marine désignant des points de repère remarquables). Ces points correspondent à des objets de l'environnement de taille suffisamment petite, ou situés suffisamment loin du robot, pour pouvoir être considérés comme ponctuels (Figure 9.3, à gauche). Ils possèdent l'inconvénient que la perception d'un point de l'environnement ne suffit pas à déterminer de manière unique la position du robot. Ce type de points de repère est par conséquent relativement pauvre et contraint à la détection de plusieurs objets pour assurer une localisation précise. De plus, reconnaître un tel point de manière non ambiguë est souvent difficile et requiert une bonne capacité de discrimination de la part des capteurs. Cependant, certains modèles ne requièrent pas cette identification et utilisent des points indistinguables.
|
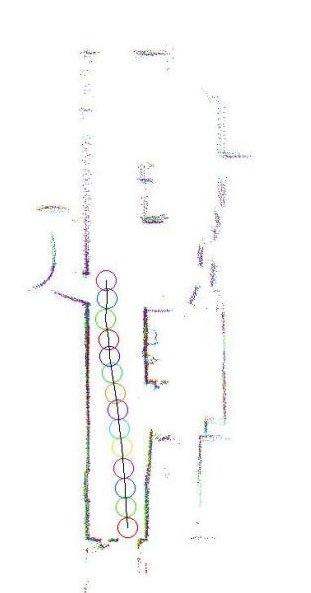
Figure 9.3 - Exemples de cartes métriques à base de points isolés (on parle alors d'amers, à gauche, repris de [109]) et de carte à base de scans lasers (chaque cercle est le centre d'un scan laser regroupant les points de la même couleur, à droite). |
|
Certains modèles ont recours à des ensembles de points disséminés sur la surface des objets de l'environnement [94, 63, 134] (Figure 9.3, à droite). Ces points sont en général obtenus par des télémètres laser, qui permettent d'en recueillir un grand nombre avec une résolution spatiale élevée. Les objets sont ainsi définis par la configuration d'ensembles de points, et non plus par des points uniques. Cette méthode présente donc l'avantage de ne pas recourir à l'identification individuelle de chaque point.
Points orientés
Afin d'obtenir plus d'informations sur la position du robot par la perception d'un seul objet, il est possible de doter chaque objet ponctuel d'une orientation. La perception d'un tel point orienté permet alors d'estimer la position du robot de manière unique. Un tel type de point peut correspondre à un point de référence sur un objet non ponctuel de l'environnement [68, 129], par exemple l'angle d'un obstacle, perçu grâce à un télémètre laser [18].
Frontière des objets
|
Figure 9.4 - Exemple de carte à base de segments détectés par un télémètre laser (repris de [52]). |
Les frontières des différents objets et obstacles de l'environnement peuvent être directement représentées par des objets géométriques de plus haut niveau que des points. Des lignes ou des polygones sont très souvent utilisés (Figure 9.4). Ces objets sont extraits d'ensemble de points perçus par des capteurs à ultrasons [39, 53] ou des télémètres laser [103, 41, 28, 52]. Des cylindres et des plans, détectés par des capteurs à ultrason sont aussi utilisés [92], ainsi que des structures de plus haut niveau, comme des plans en trois dimensions, détectés par stéréovision [8].
Représentation de l'incertitude
Dans la plupart des systèmes, la manière dont est représentée et gérée l'incertitude est cruciale. L'incertitude concernant les objets mémorisés dans la carte est de deux types. Le premier concerne l'incertitude sur les paramètres des objets, par exemple sur leur position dans l'environnement. Ce type d'incertitude provient des erreurs de localisation du robot lors de la perception d'un objet, ou d'un bruit au niveau du capteur. Il est, dans la majorité des cas, représenté de manière probabiliste, notamment par la variance de paramètres considérés [129, 8, 103, 92, 68, 44, 28]. Toutefois, d'autres méthodes peuvent être utilisées, par exemple des intervalles [43] ou des ensembles flous [53].
Le second type d'incertitude se place à un niveau plus fondamental. Il porte sur la qualité de la correspondance entre la carte et l'environnement. Il mesure avec quelle confiance un objet présent dans la carte correspond effectivement à un objet de l'environnement. En effet, il peut arriver que des erreurs de perception fassent apparaître des objets qui n'existent pas dans l'environnement. Cette incertitude est caractéristique des environnements dynamiques, dans lesquels des objets sont susceptibles de se déplacer, d'apparaître ou de disparaître. Elle est gérée, pour une grande partie, au niveau des capteurs, les procédures permettant la détection d'objet à mémoriser étant conçues pour ignorer au maximum les éléments instables de l'environnement. Au niveau de la carte, la plupart des modèles traitent ce problème au moment de la mise à jour. Il est par exemple possible de supprimer les objets qui auraient dû être perçus, mais qui restent introuvables par le robot. Certains modèles toutefois modélisent explicitement cette incertitude au moyen d'un paramètre de crédibilité [92]. Ce paramètre permet une plus grande tolérance aux accidents de perception en mesurant la fiabilité d'objets comme point de repère.
IV-B-2-d-ii. Représentation de l'espace libre▲
Un des premiers modèles pour ce type de représentation est celui de la grille d'occupation [101, 131, 147]. Dans ce modèle, l'environnement est entièrement discrétisé suivant une grille régulière avec une résolution spatiale très fine (cf. Figure 9.5). Une probabilité d'occupation est associée à chaque élément de cette grille. Cette probabilité mesure la confiance dans le fait que l'espace correspondant dans l'environnement est effectivement occupé par un obstacle. L'avantage d'une telle représentation est qu'elle utilise directement les valeurs des capteurs de distance afin de mettre à jour les probabilités d'occupation des cellules. Elle permet donc de supprimer la phase d'extraction d'objets qui est souvent coûteuse en temps de calcul et source de bruit.
|
Figure 9.5 - Un exemple de grille d'occupation utilisée pour représenter un environnement. Les zones sombres indiquent une forte probabilité de présence d'un obstacle (repris de [131]). |
Les grilles d'occupation utilisent cependant une quantité de mémoire importante, qui croît proportionnellement à la surface de l'environnement. Pour s'affranchir de ce problème, certains modèles font appel à des discrétisations irrégulières de l'espace [5] ou à des discrétisations hiérarchiques. De telles discrétisations permettent de s'adapter à la complexité de l'environnement, en représentant de manière grossière les grands espaces libres et plus finement les contours des obstacles.
IV-B-3. Représentations hybrides et hiérarchiques▲
Au-delà des deux grandes catégories topologiques et métriques, il existe toute une gamme de représentations hybrides mélangeant ces deux approches.
Nous avons déjà mentionné un premier type de représentations pouvant être considérées comme hybrides : les représentations topométriques qui sont des cartes topologiques contenant des informations métriques sur les arêtes du graphe (Figure 9.2, à gauche). Ce type de représentation est par exemple bien adapté pour construire des cartes à partir de la vision : chaque nœud du graphe peut être associé à une image, relié à ses voisins par des informations obtenues par l'odométrie du robot ou par odométrie visuelle [13].
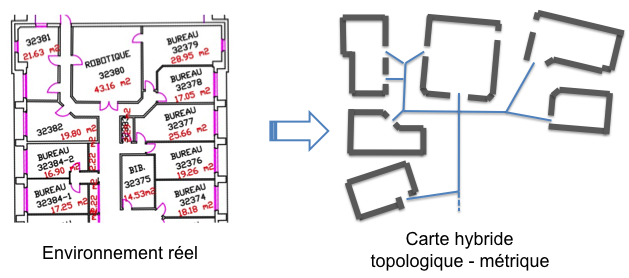
Les nœuds de la carte topométrique peuvent aussi contenir des informations plus complexes, telles que des cartes métriques locales (par exemple [136] et Figure 9.6). L'intérêt de ces représentations est de contenir des cartes métriques précises pour des zones plus simples à cartographier et dans lesquelles la navigation devra être précise (notamment les pièces) et de ne représenter les couloirs (plus difficile à cartographier du fait de leur taille et du manque de points de repère) que comme liens topologiques entre pièces. Ces cartes présentent ainsi l'avantage de ne pas demander une localisation très précise sur une zone très étendue.
|
Figure 9.7 - Un exemple de carte hiérarchique se basant sur une carte métrique dont est extraite une carte topologique. Les nœuds de cette carte topologique sont ensuite associés à une catégorie (repris de [112]). |
Enfin, au-delà des cartes brutes construites par les méthodes que nous allons présenter dans ce cours, il devient de plus en plus important d'introduire différents niveaux d'informations dans les cartes pour s'adapter aux différentes tâches d'un robot de service par exemple. En particulier, il commence à apparaître des cartes contenant des informations sémantiques. Ces informations se situent à un niveau plus haut que l'espace libre ou les obstacles représentés dans les cartes brutes et peuvent concerner par exemple les pièces détectées dans l'environnement, le type de ces pièces (cuisine, salon…) ou les objets présents dans l'environnement [97, 72, 112]. Ces types de représentations sont souvent hiérarchiques : sur la base d'une carte métrique, une carte topologique est construite, puis les nœuds sont classifiés suivant leur type et permettent de mémoriser les objets associés (Figure 9.7). Les informations sémantiques peuvent être utiles dans de nombreuses situations, par exemple pour chercher un objet (une assiette sera plus probablement dans la cuisine), ou pour la navigation : la connaissance du type d'obstacle peut ainsi permettre d'envisager de pousser certains objets tels que les chaises.
Nous ne détaillerons pas dans ce cours la construction de ce type de cartes, car elles font en général appel à l'intégration de très nombreuses méthodes différentes et sont l'objet de recherches très actives.
IV-C. Localisation▲
Ce chapitre présente les principales méthodes de localisation. On pourra trouver une description succincte d'un grand nombre d'autres méthodes dans [45]. La présentation est réalisée selon une classification personnelle en trois grandes catégories qui me semble utile à la compréhension, mais qui n'est pas forcement utilisée couramment dans la littérature.
IV-C-1. Différentes capacités de localisation▲
Il existe trois types de capacités regroupées sous le terme « localisation », de complexités différentes.
- Le suivi de position est la capacité de mettre à jour une estimation existante de la position au vu de données proprioceptives ou de perceptions nouvellement acquises. Dans le cas des données proprioceptives, cette mise à jour concerne un déplacement du robot et va en général diminuer la précision de l'estimation courante de la position, à cause de l'erreur sur la mesure. Dans le cas de perceptions, au contraire, cette mise à jour va en général permettre d'améliorer cette estimation grâce au lien avec l'environnement fourni par ces données. L'utilisation de cet ancrage dans l'environnement est fondamentale pour assurer que l'estimation de la position reflète correctement la position du robot dans l'environnement réel. Cette mise à jour intégrant les deux types de données permet de combiner les avantages inhérents aux deux types d'informations afin d'estimer au mieux la position du robot. En pratique, toutefois, le suivi de position est problématique, car il repose sur une estimation initiale de la position qui doit souvent être fournie par une source extérieure. De plus, si la position estimée s'écarte trop de la position réelle du robot, il peut très bien être impossible de parvenir à corriger l'erreur et de retrouver la position réelle, ce qui conduit à une dérive de l'algorithme.
- La localisation globale, est plus générale et permet de retrouver la position du robot sans qu'aucune estimation initiale ne soit fournie. Cette capacité est très importante du point de vue de l'autonomie, car elle permet au robot de trouver sa position initiale, dans toutes les conditions, sans intervention extérieure. Elle permet, par exemple, de couper l'alimentation d'un robot à des fins de maintenance, puis de remettre ce robot dans une position quelconque de l'environnement sans se soucier d'initialiser correctement son estimation de la position.
- La troisième capacité est la capacité à retrouver la position d'un robot kidnappé, c'est-à-dire d'un robot dont on a une estimation de la position, mais dont l'estimation est fausse, car il a été déplacé, sans que le système de localisation n'en soit informé. Par rapport à la localisation globale, ce cas présente la difficulté supplémentaire de parvenir à détecter que la position actuellement suivie n'est plus correcte. Cette phase est délicate, car il faut distinguer entre les cas où les perceptions sont simplement temporairement bruitées, sans que le robot ait été déplacé, et les cas où le robot a réellement été déplacé.
Les capacités de suivi de position et de localisation globale ont des propriétés duales. Comme le note Piasecki [110], dans le contexte d'une carte métrique, le suivi de position est une méthode locale, continue, qui effectue régulièrement de petites corrections à l'estimation de la position du robot. Cette méthode effectue de telles corrections en se basant sur des objets de l'environnement et la manière dont ils ont été perçus par le robot. L'identification de ces objets est de plus simplifiée grâce à l'estimation initiale de la position qui permet, en cas de perceptual aliasing, de décider quel est l'objet qui a été perçu parmi les différents objets correspondant aux perceptions.
Au contraire, la localisation globale est une méthode globale, discontinue, qui effectue exceptionnellement des corrections de grande ampleur de la position estimée. Sa première tâche, avant d'estimer une position, est de déterminer à quels objets de l'environnement correspond chacune des perceptions du robot. Cette tâche peut être très simple dans le cas où la carte ne contient que des amers différents, mais est en général assez complexe, car plusieurs amers sont identiques à cause du perceptual aliasing.
Comme nous l'avons souligné, le suivi de position permet de fusionner et de tirer parti des informations proprioceptives et des perceptions disponibles pour le robot. Cette méthode ne conduit toutefois qu'à une estimation qui est localement la meilleure approximation possible de la position. En effet, la recherche est contrainte par l'estimation précédente de cette position. La position estimée sera donc celle qui est le plus en accord avec les données recueillies, dans le voisinage de cette estimation précédente. L'estimation résultante peut donc très bien ne pas correspondre à la position qui, sur l'ensemble de la carte, correspond le mieux aux données.
En principe, la localisation globale permet une telle estimation optimale. Au niveau de l'utilisation des données disponibles pour le robot, il existe de nouveau deux classes de méthodes de localisation globale :
- la première, qui ne fonctionne que dans des environnements où il n'existe aucun perceptual aliasing, fait appel uniquement aux perceptions disponibles en une position donnée. Nous l'appellerons dans ce cours inférence directe de position ;
- la seconde, qui fonctionne dans tous les environnements, fusionne au contraire les informations proprioceptives et les perceptions, comme le fait le suivi de position. Toutefois, au lieu de restreindre la recherche par une estimation précédente de la position, elle estime parmi toutes les positions possibles au sein de la carte celle qui correspond le mieux aux données présentes et passées recueillies par le robot. Les méthodes de cette catégorie reposent, d'une façon ou d'une autre, sur le suivi de plusieurs hypothèses de position, ce qui permet de généraliser le suivi de position en utilisant de manière plus efficace les informations disponibles.
Dans la suite de ce chapitre, nous allons présenter plus précisément les différentes méthodes de localisation. Nous allons d'abord voir comment il est possible d'estimer la position d'un robot au vu des seules perceptions (section III.C.2Estimation de la position par les perceptions). Puis, dans le cas de systèmes perceptifs soumis au perceptual aliasing, nous verrons comment il est possible d'intégrer les informations proprioceptives, de manière locale (section III.C.3Suivi d'une hypothèse unique) puis globale (section III.C.4Suivi de plusieurs hypothèses), afin de lever les ambiguïtés restantes.
IV-C-2. Estimation de la position par les perceptions▲
Dans cette section, nous résumons les différentes méthodes qui peuvent être utilisées pour estimer la position d'un robot à l'aide des seules perceptions. Dans le cas où l'environnement est exempt de perceptual aliasing, cette étape suffit à déterminer la position du robot de manière unique. Cette méthode est alors la première méthode de localisation globale mentionnée précédemment. Dans le cas où le perceptual aliasing est présent, ces méthodes sont également utilisées, mais elles serviront à repérer plusieurs positions possibles pour le robot au sein de l'environnement. Le suivi de position ou la seconde méthode de localisation globale qui seront présentés dans les paragraphes suivants doivent alors être utilisés en sus pour sélectionner la position correcte.
IV-C-2-a. Cartes topologiques▲
Dans le cas des cartes topologiques, estimer la position à partir des seules perceptions est extrêmement simple. En effet, parmi tous les lieux représentés dans la carte, la position du robot est celle d'un des nœuds qui correspond le mieux aux perceptions courantes. La recherche de ces nœuds passe donc par la comparaison des perceptions du robot avec les perceptions mémorisées dans chacun des nœuds de la carte. Les nœuds qui sont identiques ou suffisamment similaires sont alors reconnus comme positions possibles du robot.
En l'absence de perceptual aliasing, tous les nœuds de la carte correspondent à des situations différentes. Cette étape est alors suffisante pour la localisation complète du robot, car le nœud reconnu est unique. Différents systèmes perceptifs ont été utilisés pour implanter de tels modèles. Certains auteurs utilisent des images panoramiques de l'environnement pour définir les nœuds de la carte [80, 51]. D'autres modèles utilisent les directions ou les distances d'amers ponctuels tous discernables, soit en simulation [25, 93, 139, 124], soit sur des robots réels [9, 54].
L'utilisation d'images panoramiques permet par exemple de réaliser un système de localisation à partir d'une méthode d'indexation d'images [128]. Il suffit en effet d'avoir une base de données indexant les images des différents nœuds de la carte, puis, pour se localiser, de rechercher dans cette base l'image la plus proche de l'image courante. Cette image nous donnera le nœud correspondant à la position courante. L'indexation peut par exemple utiliser une analyse en composantes principales(9) qui va déterminer une base sur laquelle il sera possible de projeter chaque image. Les coordonnées de chaque image dans cette base fournissent ainsi une représentation de faible dimension de chaque nœud de la carte. Pour la localisation, il suffit de projeter l'image courante sur la base et de chercher l'image ayant les coordonnées les plus proches.
Lorsqu'une position dans un espace métrique est associée à chacun des nœuds de la carte, la localisation permet en outre de déterminer la position métrique du robot. Cette position peut simplement être la position du nœud reconnu, mais il est souvent possible d'obtenir une précision supplémentaire. En effet, au lieu de tenir simplement compte du nœud le plus conforme aux perceptions courantes, il est possible de tenir compte de chacun des nœuds, selon son degré de similarité avec ces perceptions. La méthode mise en œuvre dans de tels modèles pour réaliser cette estimation de position s'appelle dans la terminologie des neurosciences le codage par population de vecteurs [56]. Cette méthode consiste à estimer la position du robot par la moyenne des positions des différents nœuds, pondérées par le degré de similarité de chaque nœud avec les perceptions du robot. Cette méthode donne une estimation précise de la position du robot, mais suppose une relative continuité de l'environnement. Elle suppose en effet que des lieux similaires seront proches les uns des autres pour que la moyenne des positions ait un sens. Les perceptions doivent donc varier de manière relativement continue avec la position.
Lorsque les modèles permettent la gestion du perceptual aliasing (par une des méthodes décrites dans les paragraphes suivants), les lieux peuvent également être définis par des images panoramiques de leur environnement [6, 40, 66, 141, 113, 142], ou par la configuration des positions d'amers distants [12, 137]. Mais, puisque le perceptual aliasing sera géré par ailleurs, des définitions plus simples des nœuds peuvent également être adoptées, au prix d'une moins grande discrimination. Certains modèles utilisent ainsi les valeurs brutes de capteurs de distance [105, 98, 82, 69, 66, 108], ou la configuration des murs autour du robot afin de détecter des angles de couloirs ou des embranchements [83, 33, 125, 27, 106, 127, 130].
IV-C-2-b. Cartes métriques▲
Dans le cas des cartes métriques, diverses méthodes d'estimation de la position existent. Lorsque les perceptions sont constituées d'amers ponctuels, une méthode de triangulation peut être utilisée [14, 59, 93, 96]. Cette méthode repose sur la mesure de la direction et de la distance d'amers ponctuels connus. La perception de trois amers de ce type permet en effet de définir la position du robot de manière unique. Un simple calcul mathématique permet donc d'estimer cette position à partir des positions des amers. Ce calcul peut également être approché par des réseaux de neurones, [111], ou par des méthodes heuristiques qui permettent une meilleure résistance au bruit [144]. Lorsque cette méthode est utilisée avec des cartes ne comportant pas de perceptual aliasing, chaque amer est unique et cette méthode permet d'estimer directement de manière non ambiguë la position du robot. En cas de perceptual aliasing, certains amers ne peuvent être distingués et il faut tenir compte de l'estimation précédente de la position afin de pouvoir identifier correctement les différents amers et estimer correctement la position.
Certains types d'objets fournissent plus d'informations que des amers ponctuels, sans toutefois permettre une estimation non ambiguë de la position. Par exemple, c'est le cas des murs dont la perception fournit une information sur la distance du robot à ce mur, mais pas sur sa position le long de ce mur (cf. Figure 10.1). Certains modèles utilisent de tels types d'objets, qui permettent d'affiner une estimation précédente de la position, mais pas d'estimer directement cette position [28, 73, 117].
Lorsque les objets mémorisés dans la carte ont une certaine étendue spatiale en deux dimensions, il est par contre possible d'utiliser la perception d'un seul objet afin d'estimer directement la position du robot. Les amers utilisés peuvent alors être des objets tridimensionnels détectés par une caméra [126], les angles des obstacles détectés par un télémètre laser [7, 18, 57, 73] ou un capteur à ultrason [92, 117], des segments détectés en utilisant une caméra [8] ou un télémètre laser [28, 31, 103].
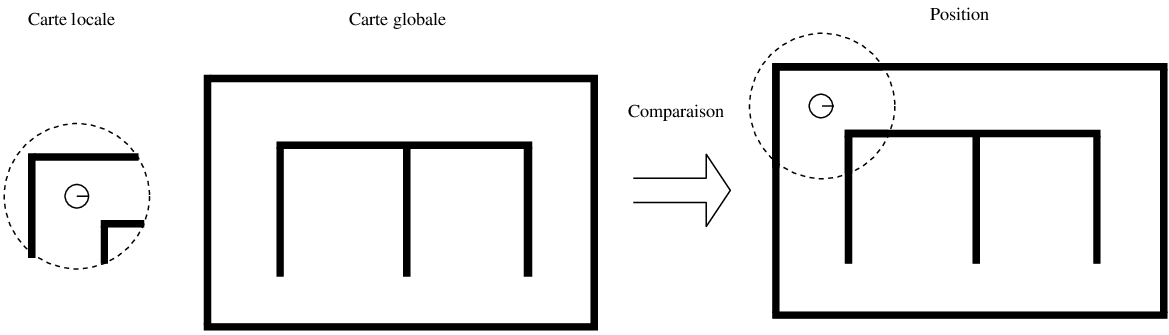
D'autres modèles enfin n'estiment pas directement la position du robot au vu des perceptions, mais reposent sur la comparaison d'une carte métrique locale avec la carte métrique globale (cf. Figure 10.2). La carte métrique locale est construite soit à partir des seules perceptions courantes, soit à partir des données proprioceptives et des perceptions recueillies sur un court laps de temps. Le problème est alors de trouver la portion de carte globale qui correspond le mieux à la carte locale. Cette méthode est très souvent utilisée avec les grilles d'occupation [107, 119, 122, 131], ainsi qu'avec des données brutes de télémètres laser [94, 65, 41]. Le polygone de visibilité, qui entoure la zone d'espace libre visible depuis la position courante du robot peut aussi être utilisé [62, 75]. Comme nous le verrons dans la section suivante, ces méthodes sont souvent utilisées sur un espace de recherche restreint par une estimation initiale de la position. Elles peuvent cependant être utilisées pour la localisation globale [107, 62, 75].
IV-C-2-c. Corrélation de cartes▲
Dans cette section, nous allons détailler une méthode de corrélation de cartes qui permet de chercher, pour deux cartes de dimensions réduites, la transformation (translation+rotation) qui permet la meilleure superposition. Cette transformation permet alors de corriger l'estimation de position du robot. Cette méthode peut être utilisée avec différents types de cartes, dont les grilles d'occupation, mais donne des résultats particulièrement efficaces avec des données issues d'un télémètre laser (Figure 10.3).
Il existe de nombreuses méthodes de mise en correspondance de scans lasers, telle que la méthode Iterated Closest Point (ICP) [95] ou des méthodes basées sur l'approche RANdom SAmple Consensus (RANSAC) [76] que nous ne présenterons pas toutes ici. La méthode que nous avons choisi de présenter [116] est une méthode simple qui est relativement robuste et résistante au bruit. Elle est basée sur les histogrammes des directions des tangentes au scan laser.
La première étape consiste à calculer pour chaque point du scan la droite tangente en utilisant la méthode des moindres carrés. On cherche pour cela la droite qui fournit la plus faible erreur quadratique sur un ensemble comprenant quelques points avant et quelques points après le point courant (Figure 10.4).
|
Figure 10.4 - Illustration de la méthode de calcul de la tangente en chaque point du scan. Pour chaque point kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, on cherche les paramètres de la droite qui donnent la plus faible erreur quadratique kitxmlcodeinlinelatexdvp\sum e_j^2finkitxmlcodeinlinelatexdvp. |
On construit ensuite l'histogramme des directions de ces tangentes, après avoir filtré les points pour lesquels la qualité de l'approximation des tangentes est trop faible. Cet histogramme contient alors des pics lorsque des ensembles de points correspondent à un mur rectiligne de l'environnement. Après avoir construit ces histogrammes de direction pour les deux scans, on cherche le décalage de ces histogrammes qui fournit la meilleure corrélation. Dans l'hypothèse où les deux scans ont été perçus en des points de l'environnement assez proches et représentent donc à peu près la même zone, ce décalage correspond à la rotation qui aligne les deux scans (Figure 10.5 gauche).
|
Figure 10.5 - Illustration de la méthode de recalage par corrélation d'histogrammes. Recalage en rotation (à gauche) et en translation (à droite). |
|
Une fois la direction recalée, pour corriger la translation, on projette les points selon la direction principale des tangentes. On construit ensuite l'histogramme du nombre de points projetés sur la perpendiculaire à cette direction et, en cherchant le maximum de corrélation entre les histogrammes correspondant aux deux scans, on corrige le décalage en translation selon cette direction (Figure 10.5 droite). On recommence ensuite cette procédure dans la direction perpendiculaire.
Cette méthode fonctionne bien dès qu'il y a des structures rectilignes dans l'environnement qui conduisent à des histogrammes contenant des pics pour lesquels le recalage par corrélation fonctionne bien. Il faut toutefois prendre un certain nombre de précautions qui ne sont pas détaillées ici, notamment faire un filtrage intelligent des scans afin de ne garder que les points qui ne correspondent ni à du bruit ni à des éléments dynamiques. Il faut également veiller à ne réaliser ce recalage que pour des scans qui ont été perçus à des positions effectivement proches, sous peine de recueillir des résultats très fantaisistes. Pour s'assurer de ce point, il est possible de vérifier la qualité de la corrélation des histogrammes afin de vérifier a posteriori que les deux scans représentaient des portions similaires de l'environnement.
IV-C-2-d. Limitations de l'estimation de la position par les perceptions▲
L'hypothèse d'un environnement sans perceptual aliasing est relativement forte, car beaucoup de capteurs en robotique sont limités et bruités. De plus, les environnements intérieurs, de type bureaux, peuvent être très réguliers et présenter de nombreuses zones apparemment similaires pour le robot. Toutefois, les environnements courants contiennent souvent suffisamment d'informations accessibles à des capteurs précis et efficaces. Un être humain, par exemple, n'a aucun mal à se repérer dans un immeuble de bureaux, en lisant les numéros écrits sur les portes (trouver son chemin jusqu'à la sortie est un autre problème !). Il est donc théoriquement possible de concevoir des systèmes suffisamment discriminants pour être capables de se repérer grâce aux seules perceptions et une carte précise. Il est de plus possible d'aménager l'environnement afin de simplifier la tâche de perception pour le robot (comme le montre l'exemple des numéros de porte). Cette solution nuit toutefois à l'autonomie du robot puisqu'il est alors limité aux environnements bien définis qui ont été préparés à l'avance. Le rejet de cette dernière solution et la difficulté de réaliser des capteurs suffisamment discriminants conduisent donc la plupart des systèmes de navigation robotique à prendre en compte le perceptual aliasing et à utiliser les données proprioceptives pour déterminer leur position de manière unique. Nous allons décrire les différentes méthodes qui peuvent être utilisées dans la suite de ce chapitre.
IV-C-3. Suivi d'une hypothèse unique▲
Lorsque les perceptions ne suffisent pas pour estimer la position de manière unique, une seconde source d'estimation de la position du robot est nécessaire pour lever l'ambiguïté. Cette seconde estimation provient, d'une part de la position déterminée lors de la précédente phase de localisation et, d'autre part, des données proprioceptives recueillies depuis cet instant. Les méthodes présentées dans cette section utilisent cette seconde estimation pour sélectionner ou calculer, à chaque instant, la position qui est la plus cohérente vis-à-vis de cette estimation. Les positions estimées grâce aux perceptions qui ne sont pas compatibles avec la position précédente sont simplement ignorées.
IV-C-3-a. Cartes topologiques▲
Dans une carte topologique, sélectionner le nœud correct parmi les nœuds correspondant aux perceptions peut reposer simplement sur l'adjacence avec le nœud précédent. Dans ce cas, le nœud sélectionné est celui qui est connecté au nœud représentant la position précédente. Cette information est toutefois rarement suffisante et les relations métriques mémorisées dans les arêtes entre nœuds sont souvent utilisées en complément. Le nœud sélectionné est donc celui dont la position relative par rapport au nœud précédent correspond le mieux aux données proprioceptives [82, 83, 33, 105]. Lorsqu'une position métrique est associée à chaque nœud, c'est le nœud dont la position est la plus proche de la position estimée par l'odométrie qui est sélectionné [12, 84, 145].
Certains modèles fonctionnent dans le sens opposé. Au lieu d'utiliser les données proprioceptives pour sélectionner un nœud parmi les nœuds possibles, ils utilisent ces données pour restreindre l'ensemble des nœuds possibles et utilisent ensuite les perceptions pour sélectionner le nœud correct parmi ceux-ci. Les perceptions sont, par exemple, utilisées pour choisir un nœud parmi tous les nœuds adjacents au nœud précédent [141], ou parmi les nœuds suffisamment proches de la position estimée par l'odométrie [142].
Enfin, certains modèles intègrent les deux étapes en une seule en calculant la probabilité que chaque nœud représente la position courante. Cette probabilité intègre, d'une part, la similarité du nœud avec les perceptions courantes, et d'autre part sa proximité avec la position estimée par l'odométrie. Le nœud ayant la plus forte probabilité peut alors être reconnu [98], ou la position peut être estimée par codage par population de vecteurs en utilisant les probabilités calculées [6, 137].
IV-C-3-b. Cartes métriques▲
Dans une carte métrique, l'estimation initiale de la position est utilisée pour restreindre l'espace de recherche de la position correspondant aux perceptions. Dans le cas où la carte contient des objets, une estimation de la position permet de simplifier le problème de l'appariement entre les objets perçus et ceux de la carte. En effet, dans le cas où les senseurs sont soumis à un fort perceptual aliasing, de nombreux objets identiques, situés à des positions différentes, sont présents dans la carte. Lorsque le robot perçoit un objet, déterminer quel objet a été perçu exige d'examiner un grand nombre de possibilités. L'estimation de la position du robot permet donc d'estimer la position des objets perçus et donc de déterminer à quels objets de la carte ils correspondent. Ce choix se fait en général en appariant simplement chaque objet perçu à l'objet mémorisé identique le plus proche [8, 28, 31, 39, 57, 92, 103, 129, 144]. Une fois l'appariement effectué, les objets sont identifiés sans ambiguïté et permettent donc d'estimer la position de manière unique.
Lorsque la position est déterminée par la mise en correspondance d'une carte locale et d'une carte globale, la position estimée est utilisée pour restreindre la recherche de la position donnant la meilleure correspondance entre les deux cartes [119, 122, 131, 147]. La recherche du maximum de correspondance est simplement effectuée sur une zone limitée autour de la position estimée précédemment. La zone étant de faible étendue, le problème de perceptual aliasing se pose moins et la recherche conduit en général à une position unique.
Lorsque la position correspondant aux perceptions a été identifiée de manière unique, elle peut être considérée directement comme la nouvelle estimation de la position du robot [147, 57, 144]. Cependant la plupart des modèles considèrent que cette estimation est entachée d'erreur, de la même manière que l'estimation initiale provenant de l'odométrie. La nouvelle position du robot est donc en général une combinaison de ces deux positions. La plupart des modèles [8, 129, 103, 31, 92, 119, 14, 18, 94, 28] utilisent un filtre de Kalman [99] pour réaliser cette combinaison. Ce filtre permet de calculer une estimation optimale de la position du robot, connaissant les deux positions et leur covariance respective. Il constitue une méthode classique de localisation et est décrit en détail dans la section III.C.3.cFiltrage de Kalman pour la localisation. D'autres méthodes sont également utilisables pour combiner ces deux informations, par exemple la minimisation d'une fonction de coût reliée à ces deux positions [131], ou l'utilisation de la méthode des moindres carrés récursifs [16].
IV-C-3-c. Filtrage de Kalman pour la localisation▲
IV-C-3-c-i. Principe▲
Le filtre de Kalman [99] permet d'estimer l'état d'un système à partir d'une prédiction bruitée de son évolution et de mesures bruitées de cet état. C'est un filtre récursif optimal, qui suppose que le système considéré est linéaire et les bruits blancs (de moyenne nulle). Pour la localisation en robotique mobile, l'état du système est la position du robot, la prédiction de l'évolution proviendra des données odométriques et les mesures proviendront des perceptions, qui permettent de calculer la position grâce à la carte. Dans la suite, nous présentons succinctement la description mathématique du filtre avant de donner un exemple d'application.
Le filtre donne à chaque instant une estimation kitxmlcodeinlinelatexdvp\hat{X}_tfinkitxmlcodeinlinelatexdvp de la valeur de l'état kitxmlcodeinlinelatexdvpX_tfinkitxmlcodeinlinelatexdvp du système, ainsi qu'une estimation de la précision de cette estimation sous forme de sa matrice de covariance kitxmlcodeinlinelatexdvpP_tfinkitxmlcodeinlinelatexdvp(10).
L'évolution de l'état du système est modélisée par l'équation linéaire suivante :
kitxmlcodelatexdvpX_{t}=A.X_{t-1} + B.u_t + \epsilon_{evo}\quad(10.1)finkitxmlcodelatexdvpoù kitxmlcodeinlinelatexdvpAfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpBfinkitxmlcodeinlinelatexdvp sont des matrices, kitxmlcodeinlinelatexdvpu_tfinkitxmlcodeinlinelatexdvp est l'odométrie relevée par le robot ou le vecteur des commandes qui lui sont données et kitxmlcodeinlinelatexdvp\epsilon_{evo}finkitxmlcodeinlinelatexdvp est le bruit sur l'estimation de l'état, supposé d'espérance nulle et de variance kitxmlcodeinlinelatexdvpQ = E\{\epsilon_{evo}\epsilon_{evo}^T\}finkitxmlcodeinlinelatexdvp.
Une mesure kitxmlcodeinlinelatexdvpY_tfinkitxmlcodeinlinelatexdvp effectuée sur l'état du système sera donnée par l'équation linéaire :
kitxmlcodelatexdvpY_t=H.X_t + \epsilon_{obs}\quad(10.2)finkitxmlcodelatexdvpoù kitxmlcodeinlinelatexdvpHfinkitxmlcodeinlinelatexdvp est la matrice d'observation et kitxmlcodeinlinelatexdvp\epsilon_{obs}finkitxmlcodeinlinelatexdvp le bruit de mesure, supposé de moyenne nulle et de variance kitxmlcodeinlinelatexdvpP_Y=E\{\epsilon_{obs}\epsilon_{obs}^T\}finkitxmlcodeinlinelatexdvp.
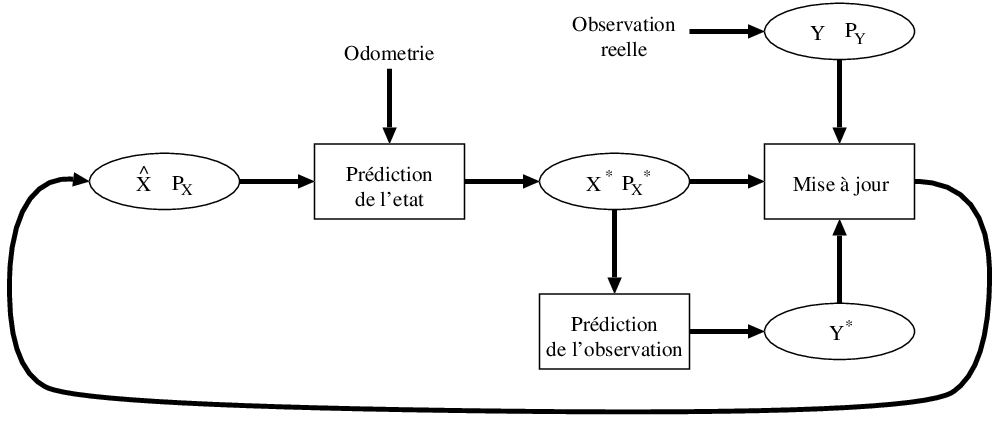
Le fonctionnement du filtre se déroule en quatre étapes (Figure 10.6) :
- Prédiction de l'état à l'instant courant kitxmlcodeinlinelatexdvpX_t^*finkitxmlcodeinlinelatexdvp, ainsi que de sa covariance kitxmlcodeinlinelatexdvpP_t^*finkitxmlcodeinlinelatexdvp à partir du modèle d'évolution, de l'estimation au pas de temps précédent et de la commande depuis cet instant:
kitxmlcodeinlinelatexdvpX_{t}^* = A.\hat{X}_{t-1} + B.u_t\quad(10.3)finkitxmlcodeinlinelatexdvp
La covariance est également prédite par la formule:
kitxmlcodeinlinelatexdvpP_t^* = A.\hat{P}_{t-1}.A^T+B.Q.B^T\quad(10.4)finkitxmlcodeinlinelatexdvp - Prédiction de l'observation à partir du modèle d'observation et de l'estimation de l'état:
kitxmlcodeinlinelatexdvpY_t^*=H.X_t^*\quad(10.5)finkitxmlcodeinlinelatexdvp - Observation de l'état: on obtient, grâce au système perceptif, une mesure kitxmlcodeinlinelatexdvpY_tfinkitxmlcodeinlinelatexdvp, dont on estime le bruit kitxmlcodeinlinelatexdvpP_Yfinkitxmlcodeinlinelatexdvp grâce au modèle du processus de perception.
- Correction de l'état prédit par mise à jour proportionnellement à l'erreur entre l'observation prédite et l'observation réalisée:
kitxmlcodeinlinelatexdvp\hat{X}_{t} = X_t^* + K(Y_t - Y_t^*)\quad(10.6)finkitxmlcodeinlinelatexdvp kitxmlcodeinlinelatexdvp\hat{P}_{t} = P_t^* - KHP_t^*\quad(10.7)finkitxmlcodeinlinelatexdvp
ou kitxmlcodeinlinelatexdvpKfinkitxmlcodeinlinelatexdvp est le gain de Kalman, calculé pour minimiser l'erreur d'estimation au sens des moindres carrés et donné par la formule :
kitxmlcodeinlinelatexdvpK = P_t^* H^T.(H.P_t^*.H^T + P_Y)^{-1}\quad(10.8)finkitxmlcodeinlinelatexdvp
Ces quatre étapes sont utilisées à chaque nouvelle information de déplacement et de perception, afin de mettre à jour l'estimation de l'état du système.
IV-C-3-c-ii. Application dans le cas d'une seule variable▲
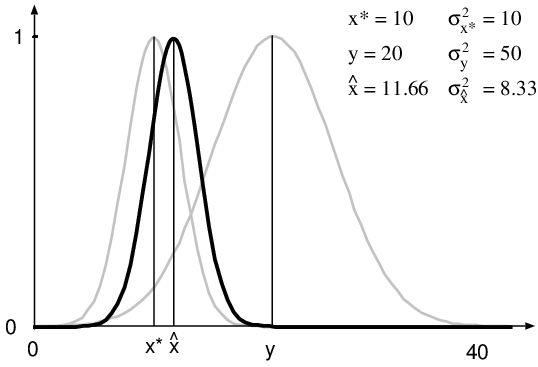
Pour montrer le fonctionnement intuitif de ce filtre, présentons son application dans un cas trivial : le cas où l'état du système est décrit par une variable scalaire kitxmlcodeinlinelatexdvpX=xfinkitxmlcodeinlinelatexdvp, de variance kitxmlcodeinlinelatexdvpP_t={\sigma_x}^2finkitxmlcodeinlinelatexdvp. Si on suppose de plus que l'observation permet d'obtenir directement la valeur de l'état : kitxmlcodeinlinelatexdvpY_t=y=xfinkitxmlcodeinlinelatexdvp avec une variance kitxmlcodeinlinelatexdvpP_Y ={\sigma_y}^2finkitxmlcodeinlinelatexdvp, le gain du filtre s'écrit simplement :
kitxmlcodelatexdvpK =\frac{ {\sigma_x^*}^2} {{\sigma_x^*}^2 + {\sigma_y}^2}finkitxmlcodelatexdvpet l'équation de mise à jour devient :
kitxmlcodelatexdvp\begin{eqnarray} \hat{x} & = & x^* + \frac{ {\sigma_x^*}^2} {{\sigma_x^*}^2 + {\sigma_y}^2}(y- x^*)&\quad(10.9)\\ & = & \frac{ {\sigma_x^*}^2 y + {\sigma_y}^2 x}{{\sigma_x^*}^2 + {\sigma_y}^2}&\quad(10.10) \end{eqnarray}finkitxmlcodelatexdvpLa mise à jour revient donc à faire une moyenne pondérée par la variance de la prédiction et de l'observation. Cette moyenne donne plus d'importance à la valeur ayant la variance la plus faible et donc la plus fiable (Figure 10.7).
|
Figure 10.7 - Illustration du filtre de Kalman dans le cas mono variable. La valeur estimée est la moyenne des valeurs prédites et observées pondérées par leur variance. Ici, l'estimation kitxmlcodeinlinelatexdvp\hat{x}finkitxmlcodeinlinelatexdvp est plus proche de kitxmlcodeinlinelatexdvpx^*finkitxmlcodeinlinelatexdvp qui une variance plus faible. |
Intuitivement, le filtre de Kalman va donc accorder plus d'importance aux valeurs pour lesquelles l'incertitude est la plus faible et les privilégier lors de la mise à jour. En pratique ces variances sont souvent basées sur des estimations empiriques (notamment en robotique pour l'odométrie et les capteurs). Il faut donc faire très attention à ne pas sous-estimer ces incertitudes de mesure, car, dans ce cas, le filtre de Kalman convergerait vers ces mesures, ce qui peut conduire à une divergence du filtre si ces mesures ne sont pas réellement aussi fiables que l'estimation de covariance le laisse penser.
IV-C-3-c-iii. Filtre de Kalman étendu▲
Le filtre présenté dans la section précédente suppose des équations d'évolution et d'observation linéaires, ce qui n'est pas le cas en robotique mobile dès que l'on représente la direction du robot. Pour étendre le filtrage aux systèmes non linéaires, le filtre de Kalman étendu linéarise simplement les équations grâce à un développement de Taylor.
Partant des équations non linéaires suivantes :
kitxmlcodelatexdvp\begin{eqnarray} X_{t} & = & f(X_{t-1},u_t) + \epsilon_{evo}&\quad(10.11)\\ Y_t & = & h(X_t) + \epsilon_{obs}&\quad(10.12) \end{eqnarray}finkitxmlcodelatexdvpon utilise les matrices jacobiennes A, B et H définies par :
kitxmlcodelatexdvp\begin{eqnarray} A_{ij} = \frac{\partial f_i}{\partial x_j} &\quad(10.13)\\ B_{ij} = \frac{\partial f_i}{\partial u_j}\\ H_{ij} = \frac{\partial h_i}{\partial x_j}&\quad(10.14) \end{eqnarray}finkitxmlcodelatexdvpAvec ces deux matrices jacobiennes, le principe du filtre de Kalman reste exactement le même, en remplaçant simplement les équations du filtre de Kalman original par les équations suivantes :
kitxmlcodelatexdvp\begin{eqnarray*}X_{t}^* & = f(X_{t-1},u_t)\quad(10.15) \\ P_t^* & = A.\hat{P}_{t-1}.A^T+B.Q.B^T&\quad(10.16)\\ Y_t^*& = h(X_t^*)&\quad(10.17) \\ K & = P_t^* H^T.(H.P_t^*.H^T + P_Y)^{-1}&\quad(10.18)\\ \hat{X}_{t} & = X_t^* + K(Y_t - Y_t^*)&\quad(10.19)\\ \hat{P}_{t} & = P_t^* - KHP_t^*&\quad(10.20) \end{eqnarray*}finkitxmlcodelatexdvpIV-C-3-c-iv. Application à la localisation sans perceptual aliasing▲
Supposons, à titre d'exemple, un robot dont on peut commander la vitesse de translation kitxmlcodeinlinelatexdvpvfinkitxmlcodeinlinelatexdvp et de rotation kitxmlcodeinlinelatexdvp\omegafinkitxmlcodeinlinelatexdvp. L'état que l'on cherche à estimer est simplement sa position dans le plan: kitxmlcodeinlinelatexdvpX_t = (x_t,y_t,\theta_t)finkitxmlcodeinlinelatexdvp. Le vecteur de commande est kitxmlcodeinlinelatexdvpu_t=(v_t,\omega_t)finkitxmlcodeinlinelatexdvp, ce qui conduit à l'équation d'évolution du système :
kitxmlcodelatexdvpf(X_t,u_t) = \left[ \begin{array}{c} x_t+v_t.dt.cos(\theta_t) \\ y_t+v_t.dt.sin(\theta_t) \\ \theta_t + \omega_t.dt \end{array} \right]finkitxmlcodelatexdvpNous supposons de plus que le bruit entachant cette estimation est indépendant pour chaque variable et proportionnel aux vitesses :
kitxmlcodelatexdvpQ_t=\left[ \begin{array}{ccc} \sigma_T.v_t & 0 & 0 \\ 0 & \sigma_T.v_t & 0 \\ 0 & 0 & \sigma_R.\omega_t \end{array} \right]finkitxmlcodelatexdvpSupposons enfin que le système de perception permette de mesurer directement la position, par référence à la carte. L'équation d'observation sera simplement :
kitxmlcodelatexdvph(X_t)=\left[ \begin{array}{c} x_t \\ y_t \\ \theta_t \end{array} \right]finkitxmlcodelatexdvpet nous estimons un bruit constant sur cette mesure :
kitxmlcodelatexdvpP_y=\left[ \begin{array}{ccc} \sigma_{O} & 0 & 0 \\ 0 & \sigma_{O} & 0 \\ 0 & 0 & \sigma_{O_\theta} \end{array} \right]finkitxmlcodelatexdvpLes matrices jacobiennes correspondant à ces équations, obtenues en dérivant kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvphfinkitxmlcodeinlinelatexdvp sont donc :
kitxmlcodelatexdvp\begin{eqnarray*} A = \left[ \begin{array}{ccc} 1 & 0 & -v_t.dt.sin(\theta) \\ 0 & 1 & v_t.dt.cos(\theta) \\ 0 & 0 & 1 \end{array} \right] \\ H = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right] \end{eqnarray*}finkitxmlcodelatexdvpCompte tenu du fait qu'ici kitxmlcodeinlinelatexdvpH=Ifinkitxmlcodeinlinelatexdvp, l'algorithme du filtre de Kalman étendu se simplifie :
kitxmlcodelatexdvp\begin{eqnarray*} X_{t}^* & = & f(X_{t-1},u_t) \\ P_t^* & = & A.\hat{P}_{t-1}.A^T+B.Q.B^T\\ Y_t^*& = & X_t^* \\ K & = & P_t^* (P_t^* + P_Y)^{-1}\\ \hat{X}_{t} & = & X_t^* + K(Y - X_t^*)\\ \hat{P}_{t} & = & P_t^* - KP_t^* \end{eqnarray*}finkitxmlcodelatexdvpPour l'initialisation de l'algorithme, nous supposons connaître une estimation de la position du robot :
kitxmlcodelatexdvp\begin{eqnarray*} \hat{X}_0 = \left[ \begin{array}{c} x_0 \\ y_0\\ \theta_0 \end{array} \right] \\ \hat{P}_0 = \left[ \begin{array}{ccc} \sigma_{x_0} & 0 & 0 \\ 0 & \sigma_{y_0} & 0\\ 0 & 0 & \sigma_{\theta_0} \end{array} \right] \end{eqnarray*}finkitxmlcodelatexdvpet nous appliquons les équations de mise à jour pour chaque nouveau déplacement ou chaque nouvelle perception.
IV-C-3-c-v. Application à la localisation avec perceptual aliasing▲
En cas de perceptual aliasing, plusieurs valeurs de la mesure proviennent de la phase d'observation. Il faut donc choisir parmi ces valeurs la valeur correspondant à la position réelle du robot qui sera utilisée pour la mise à jour.
Lorsque l'observation donne une mesure de la position, il est possible de sélectionner simplement la mesure la plus proche de la position prédite pour le robot. Dans le cas général, il est préférable d'utiliser la distance de Mahalanobis, qui est une mesure de distance normalisée par la covariance. Cette mesure permet par exemple de privilégier une mesure plus lointaine, mais moins précise qui aura en fait une probabilité plus grande de correspondre à la mesure prédite (Figure 10.8).
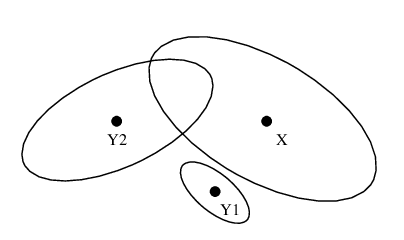
Pour deux valeurs kitxmlcodeinlinelatexdvpXfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpYfinkitxmlcodeinlinelatexdvp de covariances kitxmlcodeinlinelatexdvpP_Xfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpP_Yfinkitxmlcodeinlinelatexdvp, cette distance vaut :
kitxmlcodelatexdvpd^2 = \frac{1}{2} (X-Y)^T(P_X + P_Y)^{-1}(X-Y)\quad(10.21)finkitxmlcodelatexdvpce qui se traduit dans le cas scalaire par une simple pondération par les variances :
kitxmlcodelatexdvpd^2 =\frac{ (x-y)^2}{2(\sigma_x^2+\sigma_y^2)}finkitxmlcodelatexdvpDans le cas du filtrage de Kalman, cette distance est utilisée entre l'observation prédite et les différentes observations faites sur le système :
kitxmlcodelatexdvp\begin{eqnarray*} d^2 & = & \frac{1}{2} (Y^*-Y)^T(P_{Y^*} + P_Y)^{-1}(Y^*-Y)\\ & = & \frac{1}{2} (H.X^*-Y)^T(H.P_t^*.H^T + P_Y)^{-1}(H.X^*-Y) \end{eqnarray*}finkitxmlcodelatexdvpà partir des distances de Mahalanobis des différentes observations à l'observation prédite, il est possible de sélectionner l'observation la plus proche ou de choisir un seuil qui permettra de déterminer si une des observations correspond bien à l'état courant. Si une des observations est en dessous de ce seuil, elle est utilisée pour la mise à jour du filtre, sinon, on considère que l'état n'a pas pu être mesuré et on ne fait pas de correction de la prédiction.
L'une des principales faiblesses du filtre de Kalman pour la localisation provient précisément de cette phase d'identification (d'appariement) des éléments perçus. En effet, en cas de mauvais choix dû à une mauvaise prédiction de la position du robot ou a une erreur de perception, l'erreur d'estimation de la position sera confirmée, voire augmentée. Un tel processus conduit rapidement à une divergence du filtre et à une perte de la position du robot.
IV-C-3-c-vi. Filtre de Kalman sans parfum (unscented)▲
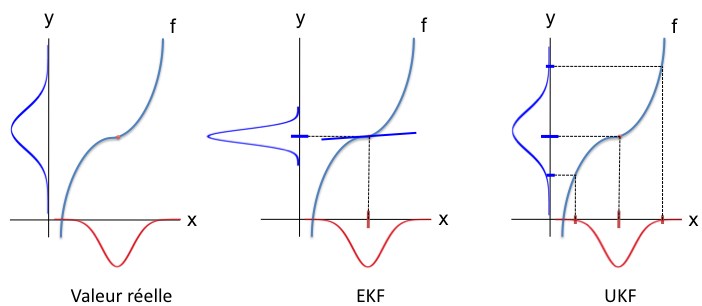
La linéarisation utilisée par le filtre de Kalman étendu peut poser problème lorsque le modèle est fortement non linéaire ou lorsque les déplacements ou les erreurs de perception sont grands. Dans certains cas, l'estimation de la covariance après transformation peut être très mauvaise (Figure 10.9). Pour ces cas-là, il existe une autre manière de linéariser les équations qui conduit au filtre de Kalman « sans parfum » (Unscented) [74].
Au lieu de linéariser l'équation non linéaire autour de la moyenne de la variable, ce filtre utilise plusieurs points d'échantillonnage à partir de la gaussienne de départ, calcule leur correspondant via l'équation non linéaire et estime la variance de la gaussienne à partir de ces correspondants (Figure 10.9). Cette stratégie permet une bien meilleure prédiction de l'état que ce soit pour l'évolution ou l'observation et permet donc d'étendre le domaine de fonctionnement du filtre de Kalman pour traiter des problèmes avec des mises à jour de plus grande ampleur. Elle est cependant plus coûteuse en calcul que le simple EKF.
IV-C-3-d. Limitations du suivi de position▲
|
Figure 10.10 - La position estimée par le suivi de position dépend fortement de l'estimation initiale de la position. Dans cet exemple, le robot mesure son déplacement dans un couloir (1 et 3) dans lequel il détecte des portes (2 et 4) sans être capable de les reconnaître individuellement (Partie kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp). Le système de localisation va estimer la position du robot en intégrant ces données. Si l'estimation initiale de la position est proche de la position correcte, le système de localisation sera capable d'estimer précisément la position réelle du robot (Partie kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp). Toutefois, si l'estimation initiale de la position est trop éloignée de la position réelle, le système fournira une estimation de la position qui n'est que localement optimale et ne correspondra pas à la position réelle (Partie kitxmlcodeinlinelatexdvpcfinkitxmlcodeinlinelatexdvp). |
La limitation principale de toutes ces méthodes de suivi de position est qu'elles ne garantissent une bonne estimation de la position que localement, autour de l'estimation initiale de la position. En pratique, si cette estimation initiale est trop éloignée de la position réelle, ces modèles ne pourront pas estimer correctement la position du robot (cf. Figure 10.10). Ces modèles ne garantissent donc pas que la position calculée soit la position de la carte qui corresponde globalement le mieux aux données recueillies par le robot et donc la position réelle la plus probable.
Ce problème prend toute son importance lorsque l'estimation de la position est perturbée à la suite d'informations proprioceptives ou de perceptions erronées. En effet, de telles informations erronées peuvent faire diverger l'estimation de la position de telle manière que le système soit par la suite incapable de retrouver une estimation correcte de la position.
La position correcte du robot pourra cependant être retrouvée par l'une des méthodes de localisation globale décrites dans la section précédente. Cette position pourra ensuite être utilisée comme nouvelle position initiale dans le processus de suivi de position. Toutefois, il est également possible d'utiliser une des méthodes de localisation globale décrites dans la fin de ce chapitre qui permettent de ne plus dépendre d'une estimation initiale correcte de la position. Cette seconde solution, qui ne requiert pas l'utilisation séparée de deux méthodes de localisation sera en général plus robuste, mais parfois moins précise.
IV-C-4. Suivi de plusieurs hypothèses▲
|
Figure 10.11 - Le suivi de plusieurs hypothèses permet de déterminer la position au sein de la carte qui globalement correspond le mieux aux données recueillies par le robot. Dans cet exemple, le robot est capable d'estimer son déplacement dans un couloir (2) dans lequel il détecte des portes (1 et 3) sans être capable de les reconnaître individuellement (Partie kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp). La perception d'une porte sans aucune estimation préalable de la position permet simplement de créer plusieurs hypothèses de position pouvant correspondre à cette perception. Il est, à ce stade impossible de décider quelle hypothèse est correcte (Partie kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp). L'intégration des données proprioceptives permet de mettre à jour la position de chacune des hypothèses, mais ne permet pas de les discriminer (Partie kitxmlcodeinlinelatexdvpcfinkitxmlcodeinlinelatexdvp). Des nouvelles perceptions permettent d'estimer la crédibilité relative de chacune des hypothèses en rendant plus crédibles les hypothèses dont la position correspond aux perceptions courantes et moins crédibles les autres. (Partie kitxmlcodeinlinelatexdvpdfinkitxmlcodeinlinelatexdvp). L'hypothèse ayant alors la plus forte crédibilité correspond à la position qui rend le mieux compte des données recueillies par le robot. |
La localisation globale, lorsque le robot est soumis au perceptual aliasing, ne peut se faire qu'en utilisant de manière optimale les informations proprioceptives et les perceptions. Contrairement au suivi de position qui utilise l'estimation précédente de la position pour sélectionner l'une des positions caractérisées par les perceptions et ignorer les autres, il faut tenir compte à chaque étape de toutes ces positions possibles. Ces positions conduisent à des hypothèses qui peuvent être mises à jour en fonction des données proprioceptives et qu'il faut comparer, afin de choisir la plus pertinente à chaque étape (cf. Figure 10.11).
IV-C-4-a. Suivi explicite de plusieurs hypothèses▲
Ce suivi de plusieurs hypothèses peut être réalisé de manière explicite, en gérant une liste des hypothèses en question. Lorsque des données proprioceptives sont disponibles, chaque hypothèse est simplement mise à jour de manière à refléter le déplacement du robot (cf. Figure 10.11c). Lorsque de nouvelles perceptions sont disponibles, l'ensemble des positions de la carte susceptibles de correspondre à ces perceptions est déterminé. Cet ensemble est ensuite comparé à l'ensemble des hypothèses. Si une hypothèse correspond à une position perçue, cette hypothèse est alors mise à jour en utilisant les perceptions par une méthode similaire à celle permettant le suivi de position, par exemple un filtre de Kalman. Les positions perçues qui ne correspondent à aucune hypothèse sont utilisées pour créer de nouvelles hypothèses associées à la position correspondante. La crédibilité de chacune des hypothèses est ensuite évaluée, généralement en fonction de la proximité de l'hypothèse avec une position correspondant aux perceptions du robot (cf. Figure 10.11d). Ainsi, une hypothèse verra sa crédibilité augmenter si elle est proche d'une des positions correspondant aux perceptions du robot, elle la verra diminuer dans le cas contraire. De nouvelles hypothèses peuvent également être ajoutées pour les positions correspondant aux perceptions qui ne correspondent à aucune hypothèse existante.
De tels modèles ont été implémentés en utilisant des cartes topologiques [37] où les différentes hypothèses correspondent à différents nœuds de la carte. Il existe également des modèles de ce type utilisant des cartes métriques [110, 73]. Ces derniers modèles utilisent en général plusieurs filtres de Kalman en parallèle et permettent de résoudre en grande partie les problèmes de divergence du filtre de Kalman employé seul. Cette technique est connue sous le nom de multi hypothesis tracking (MHT) [73].
IV-C-4-b. Filtrage bayésien▲
Les méthodes de localisation multihypothèses peuvent être vues dans un cadre plus large, celui du filtrage bayésien. Cette méthode de filtrage permet d'intégrer de manière similaire les deux types d'informations (odométrie et perceptions), mais ne gère en général pas explicitement les hypothèses de position. Les différentes hypothèses sont ici remplacées par une distribution de probabilités de présence du robot sur l'ensemble des positions possibles de la carte. Cette représentation permet donc de considérer chacune des positions au sein de la carte comme une position possible du robot dont il faut évaluer la probabilité. Nous présentons d'abord le cadre général qui permet la gestion de cette distribution de probabilités, avant de voir comment il peut être utilisé en pratique dans des cas discrets ou continus.
Le filtrage bayésien regroupe un ensemble de méthodes d'estimation d'état utilisant les probabilités et plus particulièrement la loi de Bayes :
kitxmlcodelatexdvp\begin{equation} P(X|Y)=\frac{P(Y|X)P(X)}{P(Y)}\quad(10.22) \end{equation}finkitxmlcodelatexdvpDans le cadre de la localisation en robotique mobile, kitxmlcodeinlinelatexdvpXfinkitxmlcodeinlinelatexdvp est en général la position et kitxmlcodeinlinelatexdvpYfinkitxmlcodeinlinelatexdvp une perception de l'environnement. Cette loi nous permet donc d'estimer la probabilité kitxmlcodeinlinelatexdvpP(X|Y)finkitxmlcodeinlinelatexdvp des positions, connaissant une perception, c'est-à-dire précisément ce que nous cherchons à calculer pour localiser un robot. Pour ce calcul, nous aurons besoin de kitxmlcodeinlinelatexdvpP(Y|X)finkitxmlcodeinlinelatexdvp, la probabilité d'une perception connaissant la position, qui peut être calculée grâce à la carte de l'environnement et au modèle du capteur utilisé. Nous aurons également besoin d'une estimation des probabilités des positions kitxmlcodeinlinelatexdvpP(X)finkitxmlcodeinlinelatexdvp avant cette perception, ainsi que de la probabilité globale kitxmlcodeinlinelatexdvpP(Y)finkitxmlcodeinlinelatexdvp de cette perception. Dans un filtre bayésien, cette formule est utilisée de manière récursive et kitxmlcodeinlinelatexdvpP(X)finkitxmlcodeinlinelatexdvp est donc simplement l'estimation précédente de la probabilité des positions. Quant à kitxmlcodeinlinelatexdvpP(Y)finkitxmlcodeinlinelatexdvp, il peut être remplacé par un artifice de calcul lors de l'utilisation de la formule. En effet, par la loi des probabilités marginales :
kitxmlcodelatexdvp\begin{eqnarray*} P(Y) = \sum_XP(Y|X)P(X) \end{eqnarray*}finkitxmlcodelatexdvpce qui permet d'utiliser la loi de Bayes pour calculer les probabilités kitxmlcodeinlinelatexdvpP(X|Y)finkitxmlcodeinlinelatexdvp de la manière suivante :
kitxmlcodelatexdvp\begin{eqnarray*} \forall X, temp_{X|Y} & = & P(Y|X)P(X) \\ P(Y) & = & \sum_Xtemp_{X|Y} \\ \forall X, P(X|Y) & = & \frac{temp_{X|Y}}{P(Y)} \end{eqnarray*}finkitxmlcodelatexdvpDans cette équation, le terme kitxmlcodeinlinelatexdvpP(X)finkitxmlcodeinlinelatexdvp est la probabilité a priori (prior en anglais), kitxmlcodeinlinelatexdvpP(X|Y)finkitxmlcodeinlinelatexdvp est la probabilité a posteriori (posterior en anglais). La puissance de cette équation réside dans le fait qu'elle permet de transposer une quantité simple à évaluer, kitxmlcodeinlinelatexdvpP(Y|X)finkitxmlcodeinlinelatexdvp, en une quantité plus difficile à estimer et qui nous intéresse, kitxmlcodeinlinelatexdvpP(X|Y)finkitxmlcodeinlinelatexdvp. La vraisemblance kitxmlcodeinlinelatexdvpP(Y|X)finkitxmlcodeinlinelatexdvp est simple à évaluer, car elle est le produit d'un raisonnement causal : connaissant une carte, un modèle de capteur et une position, on peut facilement prévoir les mesures que devraient renvoyer ce capteur. kitxmlcodeinlinelatexdvpP(X|Y)finkitxmlcodeinlinelatexdvp, pour sa part, est le fruit d'un raisonnement de diagnostic et il est difficile à évaluer, car une perception kitxmlcodeinlinelatexdvpYfinkitxmlcodeinlinelatexdvp ne permet pas de définir simplement une position, mais peut correspondre à plusieurs, notamment dans le cas du perceptual aliasing(11).
Nous venons de voir comment la loi de Bayes permet de mettre à jour une probabilité de position en fonction d'une perception. Pour la localisation d'un robot mobile, il faut également pouvoir intégrer l'effet d'un déplacement sur une distribution de probabilités. Cela se fait aussi très simplement grâce à l'équation suivante (loi des probabilités marginales) :
kitxmlcodelatexdvp\begin{equation} P(X|U) = \sum_{X'}P(X|U,X')P(X')\quad(10.23) \end{equation}finkitxmlcodelatexdvpDans cette équation, kitxmlcodeinlinelatexdvpP(X|U,X')finkitxmlcodeinlinelatexdvp est un modèle du déplacement du robot, qui donne la probabilité d'une position kitxmlcodeinlinelatexdvpXfinkitxmlcodeinlinelatexdvp si le robot exécute l'action kitxmlcodeinlinelatexdvpUfinkitxmlcodeinlinelatexdvp dans la position kitxmlcodeinlinelatexdvpX'finkitxmlcodeinlinelatexdvp. Ce modèle ne dépend que du robot et correspond souvent au modèle d'odométrie que nous avons vu au début du cours. Comme précédemment, la probabilité a priori, kitxmlcodeinlinelatexdvpP(X')finkitxmlcodeinlinelatexdvp, est le fruit d'une estimation à l'étape précédente.

Pour localiser un robot, nous cherchons évidemment à estimer la position à partir de nombreux déplacements et de nombreuses observations : kitxmlcodeinlinelatexdvpP(x_t|u_1,y_2,...,u_{t-1},x_{t-1})finkitxmlcodeinlinelatexdvp. Pour pouvoir réaliser les calculs de manière récursive, l'hypothèse de Markov est utilisée : on suppose que les perceptions ne dépendent que de l'état courant et que la position après un déplacement ne dépend que de la position précédente. Ceci est illustré par le réseau bayésien de la Figure 10.12 qui montre les dépendances entre variables et correspond aux simplifications suivantes :
kitxmlcodelatexdvp\begin{eqnarray*} P(y_t|x_t,u_1,y_2,...,u_{t-1}) & = & P(y_t|x_t)\\ P(x_t|u_1,y_2,...,u_{t-1},x_{t-1}) & = & P(x_t|u_{t-1},x_{t-1}) \end{eqnarray*}finkitxmlcodelatexdvpPartant de ces différents éléments, le filtrage bayésien permet donc d'estimer de manière récursive l'état d'un système à partir d'une estimation de son évolution et de mesures sur cet état. Pour pouvoir appliquer ce filtrage, nous avons besoin des éléments suivants, qui sont tous connus ou qui peuvent être définis grâce aux modèles du robot, des capteurs et de l'environnement :
- un modèle d'observation (de capteur) kitxmlcodeinlinelatexdvpP(y|x)finkitxmlcodeinlinelatexdvp qui donne, pour une position kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp donnée, la probabilité de la mesure kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp ;
- un modèle d'évolution (d'action) kitxmlcodeinlinelatexdvpP(x|u,x')finkitxmlcodeinlinelatexdvp qui donne la probabilité que le robot arrive en kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp s'il exécute l'action kitxmlcodeinlinelatexdvpufinkitxmlcodeinlinelatexdvp en kitxmlcodeinlinelatexdvpx'finkitxmlcodeinlinelatexdvp ;
- une suite d'actions et de perceptions kitxmlcodeinlinelatexdvp{u_1,y_2,...,u_{t-1},y_t} ;finkitxmlcodeinlinelatexdvp ;
- une estimation initiale de la position kitxmlcodeinlinelatexdvpP_0(x)finkitxmlcodeinlinelatexdvp, qui peut, par exemple, être uniforme dans le cas de la localisation globale ou qui peut être une répartition gaussienne si nous connaissons la position initiale du robot.
Le filtre permet d'estimer la position en fonction des données mesurées : kitxmlcodeinlinelatexdvpP(x_t|u_1,y_2,...,u_{t-1},y_t)finkitxmlcodeinlinelatexdvp, ce que nous noterons par la suite (en version continue) kitxmlcodeinlinelatexdvpBel(x_t)finkitxmlcodeinlinelatexdvp (de l'anglais Belief State). L'équation de mise à jour récursive permet alors d'estimer kitxmlcodeinlinelatexdvpBel(x_t)finkitxmlcodeinlinelatexdvp en fonction de kitxmlcodeinlinelatexdvpBel(x_{t-1})finkitxmlcodeinlinelatexdvp. Cette équation se dérive de la manière suivante, en utilisant les lois présentées ci-dessus :
kitxmlcodelatexdvp\begin{eqnarray*} Bel(x_t) & = & P(x_t|u_1,y_2,...,u_{t-1},y_t)\\ (Bayes) & = &\eta P(y_t|x_t,u_1,y_2,...,u_{t-1})P(x_t|u_1,y_2,...,u_{t-1})\\ (Markov) & = & \eta P(y_t|x_t)P(x_t|u_1,y_2,...,u_{t-1})\\ (prob totales) & = & \eta P(y_t|x_t) \int P(x_t|u_1,y_2,...,u_{t-1},x_{t-1})P(x_{t-1}|u_1,y_2,...,u_{t-1})dx_{t-1}\\ (Markov) & = & \eta P(y_t|x_t)\int P(x_t|u_{t-1},x_{t-1})P(x_{t-1}|u_1,y_2,...,u_{t-1})dx_{t-1}\\ & = & \eta P(y_t|x_t)\int P(x_t|u_{t-1},x_{t-1})Bel(x_{t-1})dx_{t-1} \end{eqnarray*}finkitxmlcodelatexdvpPour résumer, l'estimation de l'état par un filtre bayésien correspond à l'utilisation de l'équation de mise à jour suivante, pour une perception kitxmlcodeinlinelatexdvpy_tfinkitxmlcodeinlinelatexdvp et un déplacement kitxmlcodeinlinelatexdvpu_{t-1}finkitxmlcodeinlinelatexdvp:
kitxmlcodelatexdvpBel(x_t) = \eta P(y_t|x_t)\int P(x_t|u_{t-1},x_{t-1})Bel(x_{t-1})dx_{t-1}\quad(10.24)finkitxmlcodelatexdvp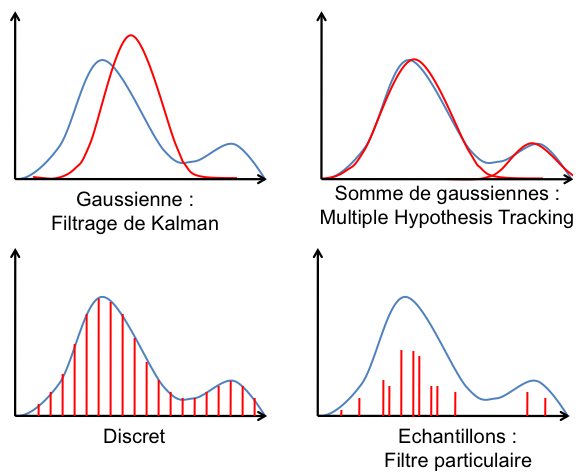
Le filtrage bayésien regroupe en fait un grand nombre d'approches connues sous des noms différents qui se différentient par la manière dont la distribution de probabilités kitxmlcodeinlinelatexdvpBel(x_t)finkitxmlcodeinlinelatexdvp est représentée (Figure 10.13). Le filtre de Kalman est par exemple une implantation de ce filtre avec des distributions de probabilités gaussiennes et des modèles linéaires. Le filtre de Kalman multihypothèse correspond à une représentation sous forme de somme de gaussiennes. Nous allons voir dans la fin de ce chapitre deux autres méthodes qui utilisent soit une représentation discrète soit une représentation sous forme d'un ensemble d'échantillons. Dans ce dernier cas, le filtre s'appelle le filtre particulaire.
Représenter la position du robot par une telle distribution de probabilités permet d'intégrer la totalité des informations recueillies au cours du temps. Elle est mise à jour, d'une part à chaque déplacement du robot, et donc à chaque nouvelle donnée proprioceptive, et d'autre part à chaque nouvelle perception. De manière imagée, les données proprioceptives permettent de déplacer les probabilités d'une position à une autre pour refléter le déplacement du robot. Les perceptions permettent de moduler la probabilité de chaque position. Ainsi, les positions pour lesquelles les perceptions prévues à l'aide de la carte sont similaires aux données perçues voient leur probabilité augmenter, tandis que les autres voient leur probabilité diminuer.
Lorsqu'on utilise une telle distribution de probabilités, la position du robot calculée est en général donnée par l'hypothèse ayant la plus forte probabilité [66, 69, 125, 127, 24, 49]. Cependant d'autres estimations telles que la moyenne des positions pondérées par leur probabilité peuvent être utilisées [27], ou des versions intermédiaires telles que la moyenne des kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp % des meilleures positions.
La distribution de probabilités obtenue dépend faiblement des conditions initiales et peut donc être initialisée à une distribution uniforme lorsqu’ aucune information n'est disponible sur la position du robot. La position sera alors retrouvée, même si le robot est soumis à un très fort perceptual aliasing, assurant ainsi la localisation globale du robot dans tous les environnements. Ces méthodes sont extrêmement robustes en pratique et mettent en œuvre un système de localisation complètement autonome, ne dépendant d'aucune intervention extérieure [133].
Ces qualités reposent toutefois de manière importante sur le fait que la carte de l'environnement est complète. En effet, les systèmes de suivi de plusieurs hypothèses nécessitent une estimation correcte des probabilités des différentes positions possibles. Or une carte partielle de l'environnement rend difficile une telle estimation à partir des perceptions. Pour cette raison, ces systèmes sont en général utilisés pour la localisation sur des cartes construites dans une phase préalable.
IV-C-4-c. Filtrage bayésien dans le cas discret▲
Pour appliquer le filtrage bayésien que nous avons présenté dans le cas continu, il faut choisir une manière de représenter les distributions de probabilités. Une première approche consiste à discrétiser l'environnement et à donner à chaque position discrète une probabilité approximant la valeur de la distribution continue. Cette approche, également nommée Histogram Filter (je ne connais pas la bonne traduction française…), a été utilisée à la fois avec des cartes topologiques où les nœuds sont utilisés comme positions possibles, [27, 66, 69, 79, 106, 108, 125, 127, 130] et avec des cartes métriques, pour lesquelles il est possible de discrétiser l'ensemble des positions, à la manière des grilles d'occupation [24, 49, 133].


Quelle que soit la discrétisation choisie, l'algorithme reste le même. Il s'agit d'évaluer la probabilité kitxmlcodeinlinelatexdvpBel(x_i)finkitxmlcodeinlinelatexdvp que le robot soit situé sur l'état kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp de la carte. Ceci est fait par deux procédures différentes selon que l'on cherche à intégrer une perception ou des données proprioceptives. Pour une perception, on utilisera la procédure de l'algorithme 10.1. Les probabilités kitxmlcodeinlinelatexdvpP(y|x_i)finkitxmlcodeinlinelatexdvp proviennent soit d'un modèle de capteur métrique pour les grilles d'occupation, soit d'un modèle comparant une perception avec les données mémorisées dans les nœuds pour la carte topologique. Pour un déplacement on utilisera l'algorithme 10.2. La Figure 10.14, tirée de [48] montre un exemple d'évolution de la probabilité de position d'un robot.
|
Figure 10.14 - Exemple d'évolution de la probabilité de position au cours du temps. Figure tirée de [48]. |
L'implantation naïve de cet algorithme conduit à une mise à jour quadratique en fonction du nombre d'états (O(kitxmlcodeinlinelatexdvpN^2finkitxmlcodeinlinelatexdvp)), ce qui peut être rapidement lourd à calculer. Cependant, le modèle probabiliste de déplacement kitxmlcodeinlinelatexdvpP(x|u,x')finkitxmlcodeinlinelatexdvp est en général nul dès que l'on s'éloigne de la position spécifiée par la commande kitxmlcodeinlinelatexdvpufinkitxmlcodeinlinelatexdvp depuis l'état kitxmlcodeinlinelatexdvpx'finkitxmlcodeinlinelatexdvp. Si l'on note kitxmlcodeinlinelatexdvppfinkitxmlcodeinlinelatexdvp le nombre d'états pour lequel le modèle est non nul, on peut facilement écrire un algorithme en O(np), qui est donc linéaire en le nombre d'états de la carte.
IV-C-4-d. Filtrage particulaire▲
Il est également possible d'utiliser une autre méthode pour représenter une distribution de probabilités continue sur l'espace de la carte [46] sans discrétisation de la carte. Cette méthode, le filtrage particulaire est l'une des plus efficaces pour la localisation.
Pour représenter la distribution de probabilités kitxmlcodeinlinelatexdvpBel(x)finkitxmlcodeinlinelatexdvp, cette méthode utilise un échantillonnage en un ensemble de particules qui permet d'approcher la distribution. En effet, considérons que la position du robot est la position moyenne définie par la distribution de probabilités kitxmlcodeinlinelatexdvpBel(x)finkitxmlcodeinlinelatexdvp :
kitxmlcodelatexdvpPosition = \int_x x.Bel(x) dxfinkitxmlcodelatexdvp|
Figure 10.15 - À gauche : méthode de représentation d'une distribution de probabilités par des particules. Les particules sont tirées aléatoirement selon la loi à représenter. À droite : méthode de représentation d'une distribution de probabilités par des particules tirées selon une loi d'importance. Les particules sont tirées aléatoirement selon la loi kitxmlcodeinlinelatexdvp\pifinkitxmlcodeinlinelatexdvp et ont chacune un poids associé kitxmlcodeinlinelatexdvpw = f/\pifinkitxmlcodeinlinelatexdvp. |
Supposons par ailleurs que l'on soit capable de générer un ensemble de kitxmlcodeinlinelatexdvpNfinkitxmlcodeinlinelatexdvp échantillons de position kitxmlcodeinlinelatexdvp\theta_ifinkitxmlcodeinlinelatexdvp, que nous appellerons particules, selon la distribution de probabilités kitxmlcodeinlinelatexdvpBel(x)finkitxmlcodeinlinelatexdvp (Figure 10.15 gauche). On peut alors approcher la position par :
kitxmlcodelatexdvpPosition \approx \frac{1}{N} \sum_i \theta_ifinkitxmlcodelatexdvpC'est cet ensemble de particules qui va permettre de représenter la distribution de probabilités de positions du robot. Tout le problème revient alors à être capable de générer récursivement un ensemble de particules réparties selon la loi kitxmlcodeinlinelatexdvpBel(x)finkitxmlcodeinlinelatexdvp.
Dans notre cas, il est évidemment impossible a priori de générer de tels échantillons, car kitxmlcodeinlinelatexdvpBel(x)finkitxmlcodeinlinelatexdvp est une distribution inconnue que nous cherchons à évaluer. Pour pouvoir néanmoins approcher cette fonction, nous allons introduire une fonction auxiliaire kitxmlcodeinlinelatexdvp\pi(x)finkitxmlcodeinlinelatexdvp, appelée fonction d'importance selon laquelle nous allons tirer nos particules. En effet, avec de telles particules, réparties selon une loi kitxmlcodeinlinelatexdvp\pi(x)finkitxmlcodeinlinelatexdvp, il est également possible d'approcher kitxmlcodeinlinelatexdvpBel(x)finkitxmlcodeinlinelatexdvp. Pour cela, nous commençons par écrire :
kitxmlcodelatexdvpBel(x) = \frac{Bel(x)}{\pi(x)} \pi(x) = w(x) \pi(x)finkitxmlcodelatexdvpavec
kitxmlcodelatexdvpw(x) = \frac{Bel(x)}{\pi(x)}finkitxmlcodelatexdvpet donc, si nous générons les échantillons aléatoires kitxmlcodeinlinelatexdvp\theta_ifinkitxmlcodeinlinelatexdvp selon la fonction d'importance kitxmlcodeinlinelatexdvp\pifinkitxmlcodeinlinelatexdvp (connue, car nous l'avons choisie), nous pouvons estimer la position par :
kitxmlcodelatexdvpPosition = \int_x x.Bel(x) dx = \int_x x. w(x) \pi(x) \approx \frac{1}{N} \sum_i w(\theta_i) \theta_ifinkitxmlcodelatexdvpAinsi la distribution kitxmlcodeinlinelatexdvpBel(x)finkitxmlcodeinlinelatexdvp peut s'approcher sous la forme d'un ensemble de particules tirées selon une loi kitxmlcodeinlinelatexdvp\pi(x)finkitxmlcodeinlinelatexdvp, chaque particule ayant un poids associé kitxmlcodeinlinelatexdvpw(x)finkitxmlcodeinlinelatexdvp (Figure 10.15 droite). La difficulté d'échantillonner selon kitxmlcodeinlinelatexdvpBel(x)finkitxmlcodeinlinelatexdvp reste cachée dans la difficulté de calculer le poids de chaque particule kitxmlcodeinlinelatexdvpw(x)finkitxmlcodeinlinelatexdvp, mais grâce à un choix judicieux de kitxmlcodeinlinelatexdvp\pi(x)finkitxmlcodeinlinelatexdvp nous pouvons arriver à rendre ce calcul possible en utilisant l'équation de mise à jour du filtrage bayésien.
En effet, dans le cas qui nous intéresse :
kitxmlcodelatexdvp\begin{equation} Bel(x_t) = \eta P(y_t|x_t)\int P(x_t|u_{t-1},x_{t-1})Bel(x_{t-1})dx_{t-1}\quad(10.25) \end{equation}finkitxmlcodelatexdvpen choisissant (intelligemment) kitxmlcodeinlinelatexdvp\pi(x) =\int P(x|u_{t-1},x_{t-1})Bel(x_{t-1})dx_{t-1}finkitxmlcodeinlinelatexdvp, nous obtenons:
kitxmlcodelatexdvp\begin{eqnarray*} w(\theta) & = & \frac{Bel_t(\theta)}{\pi(\theta)} \\ & = & \frac{\eta P(y_t|\theta)\int P(\theta|u_{t-1},x_)Bel_{t-1}(x)dx }{\int P(\theta|u_{t-1},x_{t-1})Bel(x_{t-1})dx_{t-1}} \\ & = &\eta P(y_t|\theta) \end{eqnarray*}finkitxmlcodelatexdvpCette valeur est simple à calculer, car elle ne dépend que de la carte et du modèle de capteurs pour la position d'un échantillon kitxmlcodeinlinelatexdvp\thetafinkitxmlcodeinlinelatexdvp.

Le problème du calcul des poids est donc réglé avec ce choix de kitxmlcodeinlinelatexdvp\pi(x) =\int P(x|u_{t-1},x_{t-1})Bel(x_{t-1})dx_{t-1}finkitxmlcodeinlinelatexdvp. Reste à voir comment il est possible d'échantillonner des particules selon cette loi. Comme nous utilisons une méthode récursive, kitxmlcodeinlinelatexdvpBel(x_{t-1})finkitxmlcodeinlinelatexdvp est approchée sous la forme d'un ensemble de particules kitxmlcodeinlinelatexdvp\theta_{t-1}finkitxmlcodeinlinelatexdvp, chacune associée à un poids kitxmlcodeinlinelatexdvpw_{t-1}finkitxmlcodeinlinelatexdvp. À partir de ces particules, l'échantillonnage selon kitxmlcodeinlinelatexdvp\pi(x)finkitxmlcodeinlinelatexdvp, se déroule en deux étapes : une mise à jour selon le modèle d'évolution kitxmlcodeinlinelatexdvpP(x|u_{t-1},x_{t-1})finkitxmlcodeinlinelatexdvp, puis un rééchantillonnage des particules pour correspondre à la loi kitxmlcodeinlinelatexdvp\pi(x)finkitxmlcodeinlinelatexdvp.
Pour la première étape, les particules sont mises à jour à partir du modèle de déplacement en tirant de manière aléatoire, pour chaque particule kitxmlcodeinlinelatexdvp\theta_ifinkitxmlcodeinlinelatexdvp, une particule kitxmlcodeinlinelatexdvp\delta_ifinkitxmlcodeinlinelatexdvp selon la loi kitxmlcodeinlinelatexdvpP(x|u_{t-1},\delta_i)finkitxmlcodeinlinelatexdvp. L'ensemble des kitxmlcodeinlinelatexdvp\delta_ifinkitxmlcodeinlinelatexdvp représente alors la distribution kitxmlcodeinlinelatexdvp\int P(x|u_{t-1},x_{t-1})Bel(x_{t-1})dx_{t-1}finkitxmlcodeinlinelatexdvp, mais la fonction d'importance selon laquelle ils sont répartis n'est pas celle que nous voulons (Figure 10.16).
|
Figure 10.17 - Illustration de la méthode d'échantillonnage. L'ensemble de particules kitxmlcodeinlinelatexdvpwfinkitxmlcodeinlinelatexdvp est rééchantillonné en l'ensemble kitxmlcodeinlinelatexdvpvfinkitxmlcodeinlinelatexdvp. |
La seconde étape a pour but d'obtenir un échantillonnage selon la fonction d'importance kitxmlcodeinlinelatexdvp\int P(x|u_{t-1},x_{t-1})Bel(x_{t-1})dx_{t-1}finkitxmlcodeinlinelatexdvp. Pour cela, il faut rééchantillonner, ce qui peut se faire selon une méthode appelée Stochastic universal sampling [11]. Cette méthode consiste à choisir kitxmlcodeinlinelatexdvpNfinkitxmlcodeinlinelatexdvp particules kitxmlcodeinlinelatexdvp\delta_ifinkitxmlcodeinlinelatexdvp selon des points équirépartis sur un cercle sur lequel sont disposées l'ensemble initial des particules selon des secteurs angulaires de taille proportionnelle à leur poids (Figure 10.17). Cette méthode permet de multiplier les particules qui ont des poids élevés, et de réduire le nombre d'échantillons correspondant aux particules de poids faibles (Figure 10.18).

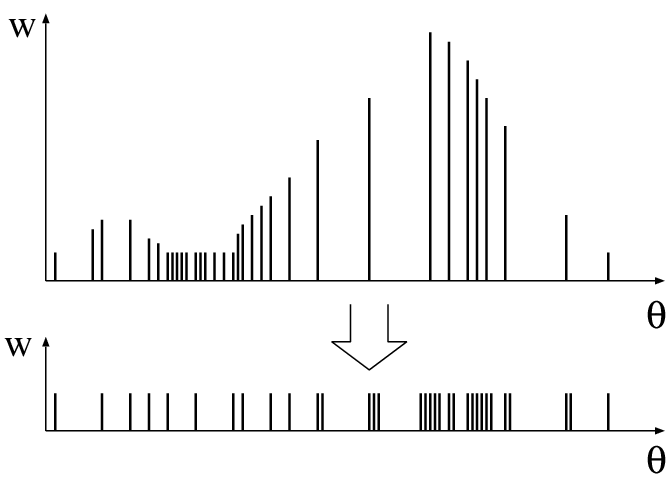
En résumé, la localisation par filtrage particulaire s'effectue selon l'algorithme 10.3, et est illustrée sur la Figure 10.19. Intuitivement, l'algorithme permet de concentrer les particules dans les zones de plus fortes probabilités, où elles auront des poids plus forts. C'est un algorithme finalement extrêmement simple et particulièrement robuste.
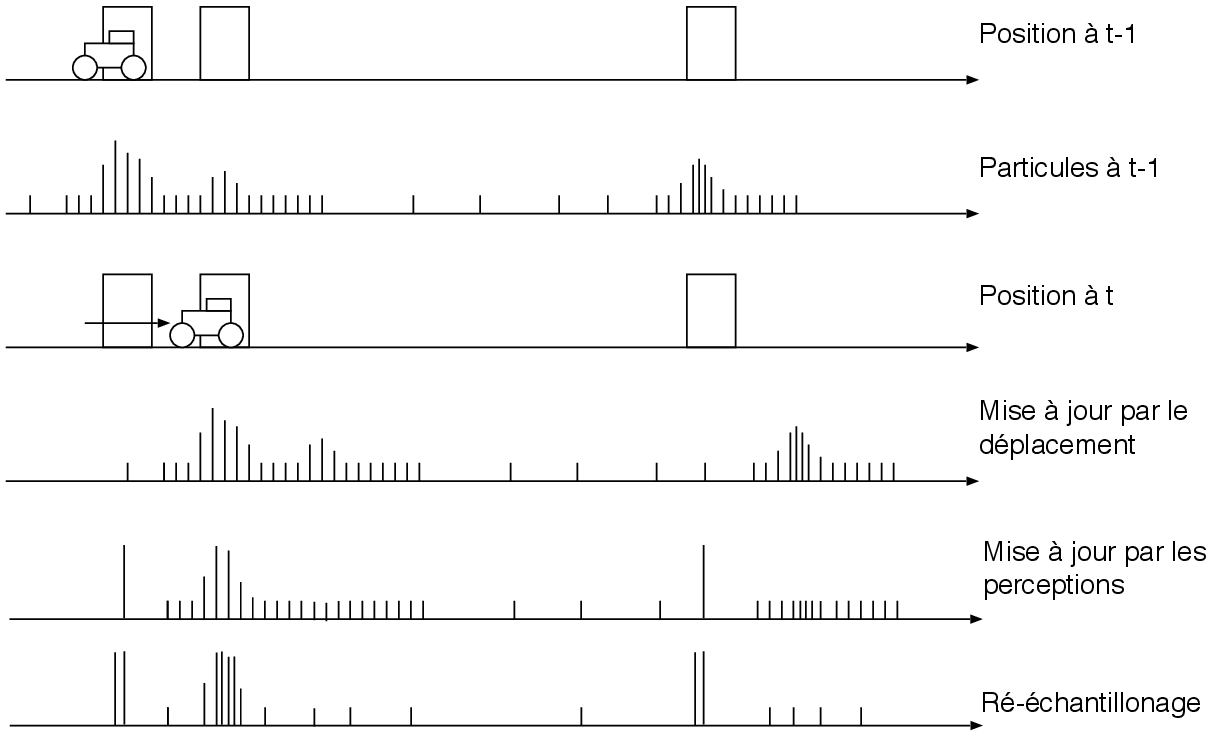
Cette version de base demande cependant un réglage relativement précis des paramètres, notamment des modèles probabilistes de perception et de l'odométrie pour donner des résultats satisfaisants.
Le nombre de particules utiles pour approcher correctement la probabilité de position peut également être relativement délicat à choisir. En effet, s'il y a trop peu de particules, les zones de fortes probabilités risquent de ne pas être bien représentées et le rééchantillonnage ne permettra pas de concentrer les particules autour de la position la plus probable, le filtre ne convergera donc pas. On parle alors de raréfaction des particules.Ce problème est d'autant plus important pour la localisation globale, pour laquelle les particules sont initialisées aléatoirement sur tout l'environnement. S'il n'y a pas initialement de particule proche de la position réelle du robot, le filtre ne pourra pas la découvrir.
Augmenter le nombre de particules permet en général de résoudre le problème, mais augmente proportionnellement le temps de calcul, ce qui est rapidement problématique. Il existe donc de nombreuses variantes et améliorations de la méthode, qui permettent par exemple de sélectionner automatiquement le nombre de particules optimal pour fournir une approximation correcte de la position [50], ou de réaliser des mises à jour partielles pour respecter un temps de calcul limite [85].
IV-C-5. Comparaison des méthodes de localisation▲
Le tableau de la Figure 10.20 résume les grandes caractéristiques et compare les différentes méthodes de localisation présentées dans ce cours.
|
Topologique hypothèse unique |
Topologique hypothèses multiples |
Métrique Filtre de Kalman |
Métrique MultiKalman |
Métrique Filtres particulaires |
|
|---|---|---|---|---|---|
|
Modèle de senseur |
Quelconque |
Quelconque |
Gaussien |
Gaussien |
Quelconque |
|
Capacité de localisation |
Suivi |
Global |
Suivi |
Global |
Global |
|
Consommation Mémoire |
++ |
++ |
+ |
+ |
++ |
|
Consommation Calcul |
+ |
++ |
+ |
++ |
++ |
|
Simplicité d'Implémentation |
++ |
+ |
+ |
- |
++ |
|
Précision |
- |
- |
++ |
++ |
+ |
|
Robustesse |
+ |
++ |
- |
+ |
++ |
Les méthodes topologiques sont en général assez simples à implanter puisqu'il s'agit essentiellement de créer une procédure de comparaison de perceptions. Cependant, pour obtenir une robustesse correcte, cette procédure doit néanmoins être faite avec soin et peut devenir complexe. La localisation directe à partir des seules perceptions est difficile à envisager dans des environnements non triviaux. L'ajout de suivi multihypothèses dans ce cadre permet cependant d'améliorer la robustesse de manière assez simple. Les cartes topologiques conduisent cependant à une localisation relativement imprécise et demandent un certain nombre de comportements sensorimoteurs efficaces pour les déplacements entre lieux. Un des gros inconvénients des cartes topologiques, comme nous le verrons plus loin, se situe plutôt au niveau de leur création, qui peut être complexe à automatiser.
Concernant les méthodes métriques, le filtre de Kalman connaît un grand succès, mais peut être difficile à régler et risque de diverger. L'utilisation de multiKalman permet d'améliorer sensiblement les choses et donne une très bonne précision, mais conduit à des implantations assez complexes et difficiles à maîtriser. Les filtres particulaires sont une bonne solution, en particulier pour leur robustesse et leur simplicité d'implantation, mais peuvent aussi être difficiles à régler et lourds en temps de calcul.
IV-D. Cartographie▲
Ce chapitre présente différentes méthodes de cartographie selon une classification personnelle en fonction de la capacité de ces méthodes à revenir ou non sur les données passées.
IV-D-1. Problèmes de la cartographie▲
IV-D-1-a. Limitation des méthodes de localisation▲
Comme nous l'avons expliqué dans le chapitre III.ALocalisation, cartographie et planification la cartographie est indissociable de la localisation, ce qui implique de disposer d'une méthode de localisation robuste pour espérer avoir une carte correcte. Ceci est le principal problème lors de la phase de cartographie, car une localisation correcte repose en général sur une bonne carte de l'environnement.
La tâche de cartographie est donc intrinsèquement plus complexe que celle de localisation. En effet, la localisation revient à rechercher, parmi les positions possibles représentées dans la carte, celle qui correspond le mieux à la position courante du robot. Cette recherche se déroule donc dans un espace fermé, car on postule que la position recherchée se trouve parmi les positions enregistrées dans la carte. Dans le cas de la cartographie, une difficulté importante provient du fait que l'estimation de la position du robot se déroule dans un espace ouvert, puisque le robot peut découvrir des zones encore inconnues. De plus cet espace est de faible dimension pour la localisation (trois en général), tandis que la construction de la carte se déroule dans un espace de beaucoup plus grande dimension. Par exemple, pour une carte de kitxmlcodeinlinelatexdvpNfinkitxmlcodeinlinelatexdvp amers 2D, il y aura kitxmlcodeinlinelatexdvp2Nfinkitxmlcodeinlinelatexdvp paramètres. Or que ce soit pour la cartographie ou la localisation, les données disponibles (odométrie et perceptions) restent les mêmes, et il faudra donc mieux les exploiter pour construire une carte.
L'incomplétude de la carte rend de plus la plupart des méthodes de localisation globale précédemment évoquées difficiles à utiliser, car elles supposent une comparaison des probabilités des différentes hypothèses de position. Or avec une carte en cours de construction, le robot peut se situer dans une zone qui n'est pas encore cartographiée et il sera donc impossible d'évaluer la probabilité de cette position. La plupart des systèmes reposent donc sur une méthode de localisation qui réalise un suivi de position. En effet, si le robot atteint un lieu qui n'est pas représenté dans la carte, il est possible, grâce à ces méthodes locales, de définir sa position par rapport à une position précédente connue au sein de la carte.
IV-D-1-b. Fermetures de boucle▲
L'utilisation de systèmes de localisation effectuant un suivi de position lors de la cartographie pose cependant certains problèmes, car comme nous l'avons vu au chapitre précédent, ces méthodes peuvent diverger et conduire à une estimation erronée de la position sans possibilité de retrouver la position réelle du robot. Ce problème est particulièrement important au cours du processus de cartographie, car les erreurs de localisation conduisent à des mises à jour erronées de la carte, ce qui peut conduire à des erreurs durables dans les futures tentatives de localisation.
Ces erreurs sont cruciales dans les environnements cycliques, c'est-à-dire dans des environnements contenant des boucles dont les différentes parties ne sont pas toutes visibles par les capteurs les unes à partir des autres (cf. Figure 11.1). En effet, dans de tels environnements, les erreurs de cartographie durant le parcours du cycle peuvent empêcher la reconnaissance de la fermeture du cycle et conduire à des cartes à la topologie erronée (cf. Figure 11.2). Il existe d'ailleurs des algorithmes spécialement adaptés à la détection de fermetures de boucle afin de pouvoir corriger ce type d'erreurs [1].
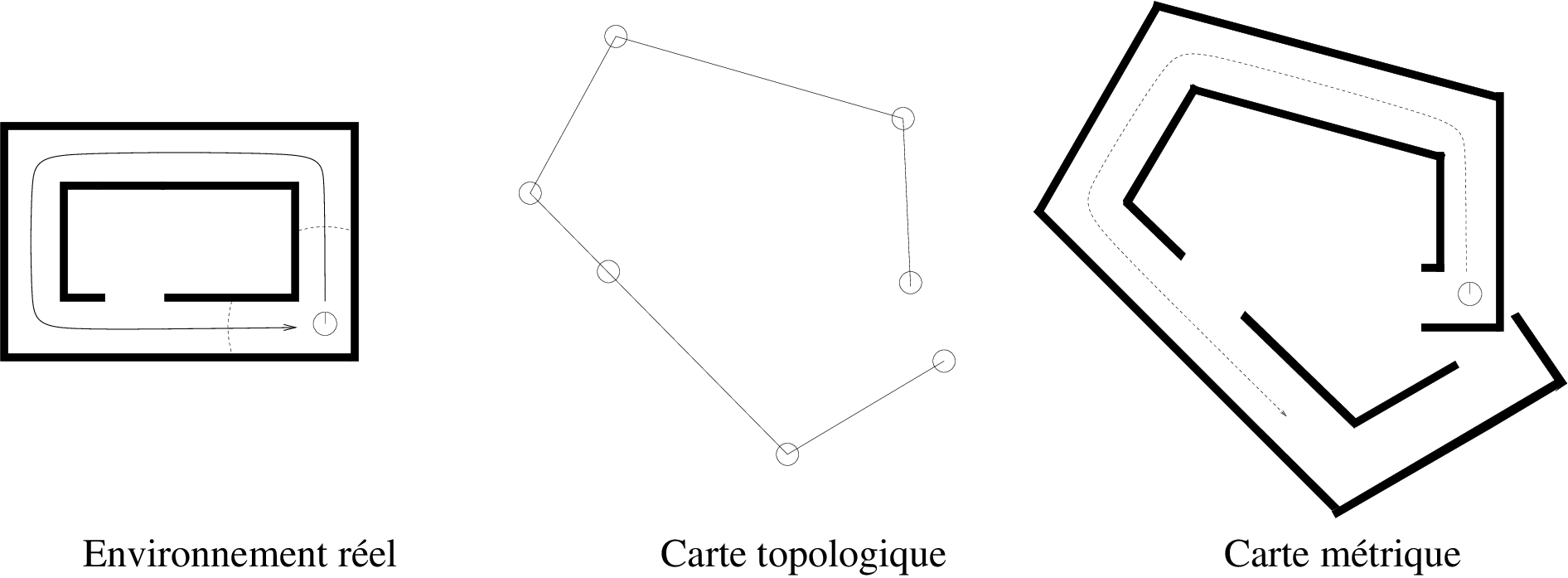
IV-D-1-c. Cartographie incrémentale et retour en arrière▲
Un autre problème important de la cartographie est le choix de la représentation utilisée pour mémoriser les informations qui serviront par la suite au robot. Nous avons déjà présenté les réponses à ce problème en présentant les diverses structures de cartes, mais il faut garder à l'esprit que le choix de cette structure a une grande influence sur la qualité du processus de cartographie. Le choix de la représentation va déterminer la possibilité de faire ou non des mises à jour globales et efficaces lorsque de nouvelles informations sont disponibles.
On peut distinguer deux grandes catégories de méthodes de cartographie. La cartographie incrémentale [134] constitue une première méthode simple de construction de carte. Elle permet simplement d'ajouter localement de nouvelles informations dans la carte à partir de l'estimation courante de la position du robot. Cependant, si cette estimation se révèle fausse a posteriori, il est impossible de revenir sur les modifications qui ont été effectuées. Cette limitation se révèle problématique dans les environnements contenant des cycles parce que la fermeture d'un tel cycle donne une information importante sur les erreurs des estimations précédentes de la position du robot. Cette information est ignorée par les systèmes de cartographie incrémentale et conduit, dans le cas d'environnements cycliques à des cartes dans lesquelles les erreurs vont se concentrer dans une petite zone (cf. Figure 11.2 et 11.3).
La cartographie incrémentale constitue la méthode de base de nombreux systèmes utilisant des cartes topologiques. Cette méthode est également utilisée pour la création de grilles d'occupation que nous décrirons plus loin.
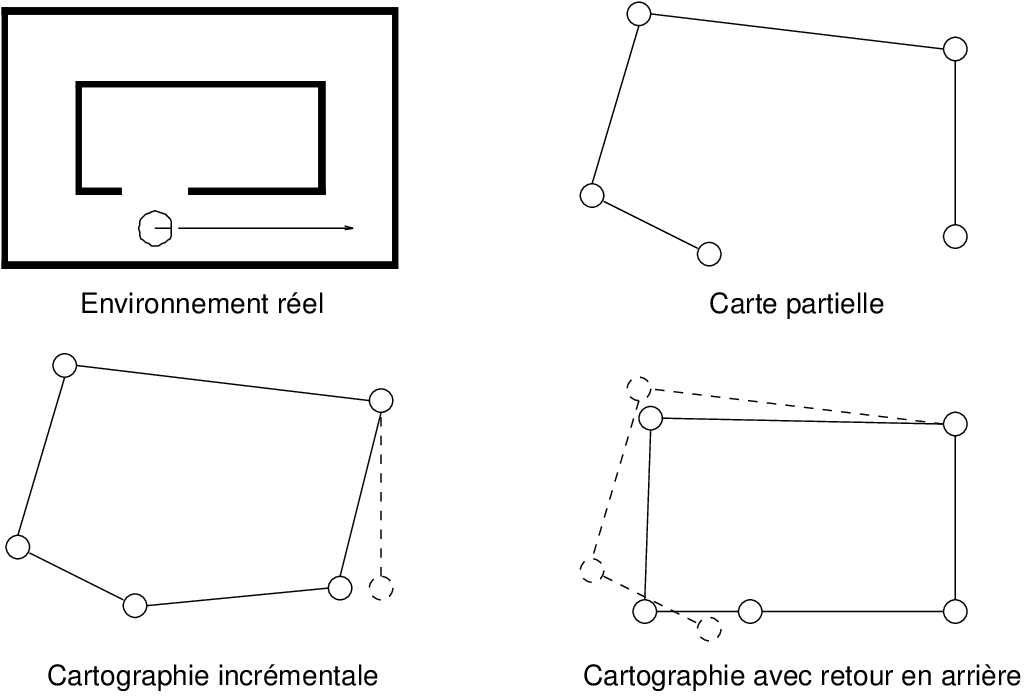
La seconde catégorie de systèmes de cartographie regroupe les systèmes qui permettent d'intégrer des informations a posteriori sur les positions passées du robot (Figure 11.3). Il faut noter que l'intégration de données a posteriori sur les positions passées est relativement simple dans les cartes topologiques grâce à la séparation des données proprioceptives et des perceptions que cette représentation implique. En effet, des erreurs dans l'estimation de la position du robot n'influent que sur les informations mémorisées dans les liens de la carte, et non sur les perceptions qui sont mémorisées dans les nœuds. Ainsi, revenir sur une modification passée de la carte, lorsque des nouvelles informations sur la position du robot sont disponibles, requiert simplement de modifier les informations mémorisées dans les liens et ne concerne pas les perceptions mémorisées. Dans le cas des cartes métriques, la modification d'une position passée va avoir des répercussions sur les perceptions (via le modèle métrique) et va donc rendre les modifications dues aux retours en arrière assez profondes. Pour permettre de tels retours en arrière, il faut alors utiliser un moyen de mémoriser les perceptions en les reliant à la position depuis laquelle elles ont été perçues. Cela peut se faire en mémorisant les perceptions indépendamment (des scans lasers par exemple), mais n'est pas possible pour certaines représentations (notamment les grilles d'occupation).
IV-D-2. Cartographie incrémentale▲
Les modèles de cartographie incrémentale utilisent donc une méthode de suivi de position pour estimer la position du robot par rapport à la carte existante. Au vu de cette position, si la carte ne représente pas le lieu ou les objets perçus par le robot, ceux-ci sont ajoutés à la carte. En revanche, si ce lieu est déjà représenté, la carte est adaptée en fonction des nouvelles perceptions.
IV-D-2-a. Cartes topologiques▲
Pour construire une carte topologique, nous commençons donc par estimer la position du robot. Dans les cartes topologiques sans perceptual aliasing [124, 25, 93, 51, 146, 55, 10], il suffit de comparer les perceptions courantes avec les données mémorisées dans chacun des nœuds de la carte. Si aucun des nœuds ne correspond suffisamment bien aux données courantes, cela signifie que le lieu n'est pas représenté dans la carte et qu'il devra donc être ajouté. Au contraire, si la similitude des données courantes avec un nœud de la carte est suffisante, ce nœud sera reconnu comme la position courante du robot. Le choix entre ces deux possibilités est le point difficile du processus de cartographie. En effet, dans le cas de la simple localisation, il suffit de trouver le nœud correspondant le mieux à la situation courante pour trouver la position du robot. Dans le cadre de la cartographie, il faut de plus utiliser un seuil pour décider si le lieu le plus similaire est la position courante du robot ou non : si la similitude est supérieure à ce seuil, le nœud est reconnu, sinon un nouveau lieu est créé. Cette utilisation d'un seuil rend le processus de cartographie potentiellement plus instable que la localisation seule.
Lorsque le perceptual aliasing est pris en compte, percevoir un lieu différent de tous les lieux mémorisés dans la carte permet toujours de conclure que ce lieu est nouveau. Mais des perceptions qui correspondent à un lieu déjà mémorisé ne sont pas suffisantes pour déterminer si le lieu est nouveau ou s'il est connu, car un lieu nouveau peut être similaire à un lieu déjà visité. La position précédente du robot doit donc être prise en compte pour déterminer si un lieu est nouveau ou s'il correspond à un nœud mémorisé. Si la position prédite par l'odométrie depuis le lieu précédent ne correspond pas au lieu déjà mémorisé, le lieu est considéré comme nouveau et ajouté à la carte [82, 43, 84, 145, 83, 142, 105, 12]. Certains modèles intègrent directement les informations perceptuelles et la position pour la reconnaissance des nœuds, se ramenant ainsi au cas où il n'y a pas de perceptual aliasing [6, 137, 33, 98].
Une fois le nœud reconnu ou créé, les perceptions sont utilisées pour corriger les données mémorisées dans ce nœud. Cela permet d'avoir une meilleure estimation des perceptions caractérisant le lieu grâce au filtrage du bruit sur ces données. Les données proprioceptives recueillies depuis le nœud précédent sont ensuite utilisées pour créer ou modifier l'arête qui joint le nœud précédent au nœud courant. Ce processus de cartographie est décrit par l'algorithme 11.1
Comme nous l'avons mentionné précédemment, dans le cas où des informations métriques sont mémorisées entre les lieux, la carte obtenue peut alors se révéler incohérente. Dans les méthodes de cartographie incrémentale, la cohérence peut être assurée par l'association d'une position à chacun des nœuds de la carte [6, 137, 33, 98, 84], ou par une adaptation locale des valeurs des liens (Figure 11.3). Dans le cas où ces valeurs seront ensuite simplement utilisées de manière locale(12), sans chercher à estimer les relations métriques entre lieux distants, le maintien de la cohérence peut être simplement négligé [82, 43].
IV-D-2-b. Cartes métriques : corrélation de scan▲
Une première méthode simple de cartographie métrique incrémentale consiste à simplement utiliser une méthode de corrélation de scans lasers ou de cartes locales. Lorsque le robot progresse dans une zone encore non cartographiée, la corrélation est simplement effectuée entre la carte locale courante et la carte locale précédente. La nouvelle carte locale est ensuite ajoutée à la carte de l'environnement à sa position estimée (Figure 11.4).
|
Figure 11.14 - Exemple de carte métrique créée par corrélation de scans. Chacun des cercles reliés par une ligne indique le centre d'un scan ajouté à la carte (repris de [32]). |
Lorsque le robot revient ensuite dans une zone déjà cartographiée après avoir parcouru une boucle, la corrélation peut être faite entre la carte locale courante et la portion de la carte globale la plus proche de la position actuelle (et non uniquement avec la carte locale précédente). Ceci permet de réestimer la position du robot dans la portion de carte déjà construite, mais ne corrige pas la carte le long de la boucle. Nous verrons plus loin (section III.D.3.aMéthodes de relaxation) comment étendre ces méthodes pour corriger ces erreurs.
Cette méthode est en général suffisante lorsqu'elle est utilisée avec les données d'un télémètre laser et dans un environnement de taille limitée ne contenant pas de grands cycles. Lors de la fermeture de grands cycles, par contre, elle montre rapidement ses limites, car les erreurs de localisation ne permettent pas de trouver la bonne portion de carte avec laquelle faire la corrélation. La méthode échoue alors, mais il est possible d'ajouter des procédures spécifiques qui font une recherche globale lorsqu'un cycle semble être fermé et permettent de rattraper ces échecs [64].
IV-D-2-c. Cartes métriques : grilles d'occupation▲
Une autre méthode de cartographie incrémentale très populaire est la construction de grilles d'occupation. Rappelons que les grilles d'occupation sont une représentation de l'environnement dans laquelle l'espace est discrétisé en cellules régulières et dont chaque cellule a une probabilité associée d'être occupée par un obstacle (Figure 11.5). La construction de grilles d'occupation est l'une des premières méthodes de cartographie à avoir été développée.
Dans les premiers travaux de leurs créateurs, Moravec et Elves [101, 131], la construction de grilles d'occupation supposait la position du robot connue. Dans des développements ultérieurs, toutefois, la grille en cours de construction est utilisée pour estimer la position du robot. On utilise pour cela des techniques de mise en correspondance de grilles similaires à celles présentées dans la section III.C.2.cCorrélation de cartes. Ces méthodes de recalage permettent de limiter la dérive de l'odométrie, mais ne sont en général pas suffisantes pour garantir une cartographie correcte dans les environnements cycliques. Pour résoudre ce problème, il est possible d'utiliser des hypothèses sur l'environnement, afin de permettre le recalage de l'odométrie durant la cartographie. L'hypothèse la plus couramment utilisée suppose que les murs de l'environnement sont rectilignes et orthogonaux [131, 83], ce qui permet de corriger facilement l'estimation de la direction du robot.
Après avoir estimé la position du robot, les valeurs des différentes cellules de la grille d'occupation sont mises à jour en fonction des perceptions. Pour cela, nous disposons d'un modèle des capteurs kitxmlcodeinlinelatexdvpP(occ_i|s)finkitxmlcodeinlinelatexdvp qui, pour une perception kitxmlcodeinlinelatexdvpsfinkitxmlcodeinlinelatexdvp donnée, nous fournit la probabilité d'occupation des cellules dans le champ de vision du capteur en fonction de la valeur renvoyée par le capteur. Ce modèle probabiliste est en général similaire à ceux présentés dans la section I.C.2.a.iiModèle probabiliste pour la distance au capteur et utilise une erreur gaussienne pour l'écart entre la direction de la cellule et la direction du capteur.
Nous cherchons donc à accumuler ces mesures pour estimer la probabilité pour la cellule kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp d'être occupée en fonction de toutes mesures précédentes : kitxmlcodeinlinelatexdvpP(occ_i^T)=P(occ_i|s_1,...,s_T)finkitxmlcodeinlinelatexdvp. Pour cela, nous utilisons, comme souvent, la formule de Bayes pour extraire la probabilité de la dernière mesure en fonction des autres variables :
kitxmlcodelatexdvpP(occ_i^T)=\frac{P(s_T|occ_i,s_1,...,s_{T-1})P(occ_i|s_1,...,s_{T-1})}{P(s_T|s_1,...,s_{T-1})}finkitxmlcodelatexdvpEn faisant l'hypothèse que le monde est statique, qui se traduit par le fait que les mesures sont conditionnellement indépendantes si l'on connaît la valeur de la cellule de la carte, nous pouvons simplifier :
kitxmlcodelatexdvpP(occ_i^T)=\frac{P(s_T|occ_i)P(occ_i^{T-1})}{P(s_T|s_1,...,s_{T-1})}finkitxmlcodelatexdvpnotre modèle de capteur nous donnant kitxmlcodeinlinelatexdvpP(occ_i|s_T)finkitxmlcodeinlinelatexdvp, nous le faisons apparaître en utilisant Bayes une nouvelle fois :
kitxmlcodelatexdvpP(occ_i^T)=\frac{P(occ_i|s_T)P(s_T)}{P(occ_i)}\frac{P(occ_i^{T-1})}{P(s_T|s_1,...,s_{T-1})}finkitxmlcodelatexdvpDans cette équation nous ne connaissons pas kitxmlcodeinlinelatexdvpP(s_T)finkitxmlcodeinlinelatexdvp ni kitxmlcodeinlinelatexdvpP(s_T|s_1,...,s_{T-1})finkitxmlcodeinlinelatexdvp. Pour pouvoir estimer kitxmlcodeinlinelatexdvpP(occ_i^T)finkitxmlcodeinlinelatexdvp, nous allons utiliser le fait que la valeur d'occupation est binaire. Nous commençons par calculer la probabilité que la cellule soit vide kitxmlcodeinlinelatexdvpP (\bar{occ}_i^T)finkitxmlcodeinlinelatexdvp, ce qui se fait de la même manière :
kitxmlcodelatexdvpP(\bar{occ}_i^T)=\frac{P(\bar{occ}_i|s_T)P(s_T)}{P(\bar{occ}_i)}\frac{P(\bar{occ}_i^{T-1})}{P(s_T|s_1,...,s_{T-1})}finkitxmlcodelatexdvpet nous permet en utilisant le rapport des deux valeurs, de se débarrasser des termes gênants.
kitxmlcodelatexdvp\frac{P(occ_i^T)}{P(\bar{occ}_i^T)}=\frac{P(occ_i|s_T)}{P(\bar{occ}_i|s_T)}\frac{P(\bar{occ}_i^{T-1})}{P(occ_i^{T-1})}\frac{P(\bar{occ}_i)}{P(occ_i)}finkitxmlcodelatexdvpet en utilisant le fait que kitxmlcodeinlinelatexdvpP(\bar{occ}_i)=1-P(occ_i)finkitxmlcodeinlinelatexdvp, nous obtenons :
kitxmlcodelatexdvp\frac{P(occ_i^T)}{1-P(occ_i^T)}=\frac{P(occ_i|s_T)}{1- P(occ_i|s_T)}\frac{1-P(occ_i^{T-1})}{P(occ_i^{T-1})}\frac{1-P(occ_i)}{P(occ_i)}finkitxmlcodelatexdvpil est alors possible d'extirper kitxmlcodeinlinelatexdvpP(occ_i^T)finkitxmlcodeinlinelatexdvp de cette expression, mais il est plus simple de chercher à estimer directement la valeur kitxmlcodeinlinelatexdvpl_ifinkitxmlcodeinlinelatexdvp définie par :
kitxmlcodelatexdvpl_i^T = log\left(\frac{P(occ_i^T)}{1-P(occ_i^T)}\right)finkitxmlcodelatexdvpqui se calcule simplement par :
kitxmlcodelatexdvpl_i^T = log\left(\frac{P(occ_i|s_T)}{1- P(occ_i|s_T)}\right)+log\left(\frac{1-P(occ_i)}{P(occ_i)}\right)+l_i^{T-1}\quad(11.1)finkitxmlcodelatexdvpCeci nous fournit une règle simple de mise à jour incrémentale des valeurs kitxmlcodeinlinelatexdvpl_i^Tfinkitxmlcodeinlinelatexdvp en fonction des valeurs précédentes et du modèle de capteur. La valeur kitxmlcodeinlinelatexdvpP(occ_i)finkitxmlcodeinlinelatexdvp est une valeur initiale de la probabilité d'occupation. Elle est en général choisie égale à 0,5 mais peut être plus faible ou plus forte si l'on souhaite intégrer un a priori sur le fait que l'environnement contient une densité plus ou moins grande d'obstacles. On retrouve ensuite la probabilité d'occupation par : kitxmlcodeinlinelatexdvpp(occ_i^T) = 1-1/e^{l_i^T}finkitxmlcodeinlinelatexdvp
Il existe également des moyens plus simples de mise à jour des grilles, qui consistent simplement à estimer la probabilité d'occupation d'une cellule en fonction du nombre de perceptions de cette cellule qui ont eu lieu. Ainsi, si on note kitxmlcodeinlinelatexdvpocc(x,y)finkitxmlcodeinlinelatexdvp le nombre de fois où un obstacle a été détecté dans cette cellule et kitxmlcodeinlinelatexdvpvide(x,y)finkitxmlcodeinlinelatexdvp le nombre de fois où cette cellule est apparue vide, car le faisceau du télémètre a traversé cette cellule, on peut simplement estimer la probabilité par :
kitxmlcodelatexdvpP_{occ}(x,y) = \frac{occ(x,y)}{vide(x,y)+occ(x,y)}finkitxmlcodelatexdvpUne variante encore plus simple pour créer une grille d'occupation est une mise à jour utilisant un simple décompte dans lequel on ajoute une certaine valeur fixe à la probabilité d'occupation d'une cellule si un obstacle y est détecté et on retranche une autre valeur fixe si la cellule a été traversée par le faisceau [78] (voir aussi la section II.B.2Méthode Vector Field Histogram). Cette méthode, nommée « histogrammic in motion mapping (HIMM) » présente cependant l'inconvénient de ne pas converger vers une valeur fixe lorsque le nombre de perceptions d'une cellule tend vers l'infini. Elle est de plus relativement sensible au bruit et suppose des réglages délicats de paramètres pour être adaptée à un robot spécifique.
IV-D-2-d. Stratégies d'exploration▲
Pour limiter les erreurs de cartographie dans ce type de méthodes, il est possible d'utiliser une exploration active de l'environnement, plutôt que de passivement mémoriser les données recueillies par le robot. Dans le cadre des cartes topologiques, il est par exemple possible, lorsqu'un nœud a été reconnu, de chercher à atteindre un des nœuds voisins mémorisés dans la carte [82]. Si ce second nœud est correctement détecté, il permet de confirmer la détection du nœud précédent qui est alors mis à jour. D'autres modèles utilisent une exploration active de l'environnement pour diriger le robot vers les zones pour lesquelles l'incertitude de la carte est grande dans le but de la réduire [42]. Enfin certains modèles sont capables de générer des hypothèses sur des portions non visitées de l'environnement qui sont ensuite vérifiées grâce à une procédure qui dirigera le robot dans les zones où de telles hypothèses ont été faites [83]. Des stratégies d'explorations peuvent également être utilisées afin de garantir une exploration rapide et exhaustive de l'environnement [131, 83, 147].
D'une manière générale, de telles procédures permettent donc, d'une part, de limiter les erreurs de cartographie en insistant sur les zones incertaines et en évitant que l'estimation de la position ne devienne trop mauvaise et, d'autre part, de garantir une exploration exhaustive de l'environnement.
IV-D-3. Retour sur les modifications passées▲
Dans les méthodes de cartographie précédentes, les modifications apportées à la carte au cours du processus de cartographie se font donc en supposant que l'estimation de la position du robot au moment de cette modification est correcte. Or cette estimation se révèle en général fausse, ou entachée d'erreur, a posteriori. Dans ce cas, les modifications de la carte ont été effectuées de manière incorrecte, et il serait souhaitable de pouvoir revenir sur ces modifications pour prendre en compte les nouveaux indices sur les positions passées du robot. La plupart des modèles de cartographie utilisés actuellement, que nous présentons dans ce paragraphe, en sont capables.
IV-D-3-a. Méthodes de relaxation▲
Une première méthode pour prendre en compte la nouvelle information de position est de propager l'erreur tout le long du cycle parcouru par le robot. Cette méthode peut s'appliquer à des cartes topologiques ou à des cartes de scans (voir section III.D.2.bCartes métriques : corrélation de scan). Intuitivement, cela correspond à identifier la carte à un réseau de ressorts, dont les positions au repos correspondent aux positions relatives des nœuds (Figure 11.6). L'erreur lors de la fermeture de boucle correspond alors à un déséquilibre dans ce réseau de ressort. Pour obtenir une carte globalement cohérente et qui respecte au mieux les positions relatives des nœuds, il suffit de calculer la position de repos du réseau de ressorts (d’où le terme de méthode de relaxation).
Il existe différents algorithmes de relaxation. Nous présentons ici un algorithme itératif très simple qui donne de bons résultats [35, 2]. Le principe de cet algorithme est de calculer la position de chaque nœud à partir de celle de ses voisins itérativement jusqu'à convergence des positions (Figure 11.7). Ainsi pour chaque nœud kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, les trois étapes suivantes sont appliquées :
- Estimation de la position du nœud kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp depuis chaque voisin kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp:
kitxmlcodeinlinelatexdvp\begin{eqnarray} (x'_{i})_j &= & x_j + d_{ji}\cos(\theta_{ji}+\theta_j)&\quad(11.2)\\ (y'_{i})_j &= & y_j + d_{ji} \sin(\theta_{ji}+\theta_j)&\quad(11.3)\\ (\theta'_{i})_j &= & \theta_j + \varphi_{ji}&\quad(11.4) \end{eqnarray}finkitxmlcodeinlinelatexdvp
et estimation de la variance du nœud kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp depuis le nœud kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp:
kitxmlcodeinlinelatexdvp(v'_{i})_j=v_j+v_{ji}finkitxmlcodeinlinelatexdvp - Estimation de la variance du nœud kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp par la moyenne harmonique des estimations depuis les voisins :
kitxmlcodeinlinelatexdvp\begin{eqnarray} v_{i} &= & \frac{n_i}{ \sum_j \frac{1}{(v'_{i})_j}}&\quad(11.5)\\ &&&\quad(11.6) \end{eqnarray}finkitxmlcodeinlinelatexdvp
où kitxmlcodeinlinelatexdvpn_ifinkitxmlcodeinlinelatexdvp est le nombre de voisins du nœud kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp. - Estimation de la position du nœud comme la moyenne pondérée des estimations depuis ses voisins :
kitxmlcodeinlinelatexdvp\begin{eqnarray} x_{i} &= & \frac{1}{n_i} \sum_j \frac{(x'_{i})_jv_i}{(v'_{i})_j}&\quad(11.7) \\ y_{i} &= & \frac{1}{n_i} \sum_j \frac{(y'_{i})_jv_i}{(v'_{i})_j}&\quad(11.8) \\ \theta_{i} &= & \arctan \left( \frac{ \sum_j{\frac{\sin((\theta'_{i})_j)}{(v'_{i})_j}}}{ \sum_j{\frac{\cos((\theta'_{i})_j)}{(v'_{i})_j}}} \right)&\quad(11.9) \\ &&&\quad(11.10) \end{eqnarray}finkitxmlcodeinlinelatexdvp
La Figure 11.8 montre un exemple de l'application de cet algorithme à une carte topométrique. Les nœuds entourés montrent les fermetures de boucle, c'est-à-dire les retours détectés à une position précédente qui sont utilisés pour contraindre le graphe.
|
Figure 11.8 - Exemple de carte topométrique obtenue par vision pour la détection de fermeture de boucle et relaxation, superposée à une carte métrique de référence obtenue par corrélation de scans lasers (tiré de [2]). |
Cet algorithme donne de bons résultats, mais peut être assez lent à converger. En effet, si l'on applique la mise à jour à tous les nœuds dans un ordre fixe (l'ordre de création des nœuds par exemple), l'erreur qui est localisée sur une seule arête au départ ne sera propagée que sur un voisin supplémentaire à chaque tour. Pour accélérer la convergence, il est possible de simplement réordonner la mise à jour des nœuds afin que l'erreur se diffuse plus rapidement.
|
Figure 11.9 - Illustration de la construction de l'arbre associé à un graphe de l'algorithme TORO (tiré de [61]). L'ordre de mise à jour optimal des nœuds pour la relaxation est donné par le parcours de l'arbre : 1, 2, 9, 3, 4, 7 … |
C'est ce que propose par exemple l'algorithme TORO (Tree-based netwORk Optimizer) [61] qui construit un arbre associé au graphe de la carte pour déterminer un ordre optimal de mise à jour. Cet arbre est construit simplement en ajoutant chaque nouveau nœud comme fils du plus ancien de ses voisins (Figure 11.9). La méthode de mise à jour de la position des nœuds est ensuite appliquée dans l'ordre donné par le parcours descendant de l'arbre. Ainsi dans l'exemple de la Figure 11.9, l'erreur(13) initialement concentrée sur l'arête entre les nœuds 1 et 9 sera propagée lors du premier parcours de la carte aux nœuds 9 et 2, puis 3, 4, 7. Avec une mise à jour dans l'ordre de création des nœuds, la propagation aurait simplement été faite aux nœuds 2, 3, 4… La première mise à jour n'aurait donc modifié que la position du nœud 9 et aurait été nulle pour les autres.
IV-D-3-b. Cartographie par filtrage de Kalman étendu▲
Le filtrage de Kalman étendu (section III.C.3.cFiltrage de Kalman pour la localisation) peut aussi être utilisé pour la cartographie. C'est cette méthode qui était à l'origine présentée sous le terme SLAM [129, 91]. Le terme SLAM est depuis devenu plus générique et la cartographie par filtrage de Kalman étendu se retrouve souvent sous le nom « EKF SLAM ».
Le filtrage est ici utilisé non seulement pour estimer la position du robot, mais aussi pour estimer la position des différents éléments enregistrés dans la carte. Cette méthode est en général utilisée avec des cartes représentant l'environnement sous forme d'objets géométriques simples tels que des points ou des segments. Elle va permettre d'utiliser les relations mesurées entre le robot et ces objets pour estimer leurs différentes positions.
Plus généralement, l'idée est donc d'utiliser un filtrage bayésien estimant à la fois les positions du robot (kitxmlcodeinlinelatexdvpx_tfinkitxmlcodeinlinelatexdvp) et des objets de la carte (kitxmlcodeinlinelatexdvpc_tfinkitxmlcodeinlinelatexdvp):
kitxmlcodelatexdvpBel(x_t,c_t) = \eta p(y_t|x_t,c_t) \int \int p(x_t,c_t|x_{t-1},c_{t-1},u_{t-1})Bel(x_{t-1},c_{t-1}) dx_{t-1} dc_{t-1}finkitxmlcodelatexdvpCette équation peut être simplifiée en utilisant l'hypothèse de monde statique, qui est utilisée dans la plupart des modèles, et qui entraîne donc que la carte de l'environnement reste la même au cours du temps (kitxmlcodeinlinelatexdvpc_t = c_{t-1}finkitxmlcodeinlinelatexdvp). Il faut bien distinguer cette hypothèse du fait que notre estimation de la probabilité des différentes cartes (kitxmlcodeinlinelatexdvpBel(x_t,c_t)finkitxmlcodeinlinelatexdvp) évolue au cours du temps, et donc que la carte que nous supposons représenter l'environnement (la plus probable en général) change au cours du temps. En utilisant cette hypothèse, l'équation du filtrage devient alors :
kitxmlcodelatexdvpBel(x_t,c_t) = \eta p(y_t|x_t,c_t) \int \int p(x_t|x_{t-1},u_{t-1})Bel(x_{t-1},c_{t-1}) dx_{t-1} dc_{t-1}finkitxmlcodelatexdvpComme pour la localisation, ce filtrage peut être implémenté de différentes manières, par exemple en utilisant un filtre de Kalman ou un filtrage particulaire (voir section suivante). Il peut également être utilisé avec différentes formes de cartes, qui rendent son implantation plus ou moins aisée. La technique communément nommée EKF SLAM consiste en l'implantation de ce filtrage sous la forme d'un filtre de Kalman étendu, en utilisant une carte contenant des amers qui peuvent être des points ou des segments. C'est historiquement la première implantation de ce type de cartographie [129].
Détaillons à titre d'exemple une implantation de cette méthode utilisant une carte contenant des amers ponctuels. Dans un état où la carte contient N amers, on utilise un vecteur d'état contenant la position du robot et des différents amers. Le vecteur d'état est donc de dimension 2N+3 :
kitxmlcodelatexdvpBel(x_t,c_t)=\left[ \begin{array}{c} x \\ y \\ \theta\\ x_{a1} \\ y_{a1} \\ \vdots \\ x_{aN} \\ y_{aN} \\ \end{array} \right]finkitxmlcodelatexdvpLa matrice de covariance associée permet de mémoriser les relations qui ont été perçues entre les amers et entre les amers et le robot. C'est l'utilisation de ces covariances lors de la mise à jour qui permettra un retour sur les modifications passées au sens où elle permettra de propager toute nouvelle information de position du robot vers les éléments dont la position relative avec le robot est connue (c.-à-d. les éléments avec lesquels la covariance est non nulle).
Supposons que l'on commande les vitesses de rotation et de translation du robot kitxmlcodeinlinelatexdvpu=(v,\omega)finkitxmlcodeinlinelatexdvp, l'équation d'évolution ne modifiera que la position du robot et sera alors :
kitxmlcodelatexdvpf(X_t,u)=\left[ \begin{array}{c} x+ v.dt.cos(\theta)\\ y+v.dt.sin(\theta)\\ \theta+\omega.dt \\ x_{a1} \\ y_{a1} \\ \vdots \\ x_{aN} \\ y_{aN} \\ \end{array}\right]finkitxmlcodelatexdvpCe qui donne la matrice jacobienne :
kitxmlcodelatexdvpA=\left[ \begin{array}{cccccc} 1 & 0 & -sin(\theta) & 0 & \dots & 0\\ 0 & 1 & cos(\theta)& 0 & \dots & 0\\ 0 & 0 & 1 & 0 & \dots & 0 \\ 0 & \dots &\dots &\dots & \dots & 0 \\ \vdots & \vdots &\vdots &\vdots & \vdots & \vdots\\ 0 & \dots &\dots &\dots & \dots & 0\\ \end{array}\right]finkitxmlcodelatexdvpenfin si l'on suppose que lors de la perception de l'amer kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, on mesure sa position relative dans le repère lié au robot en coordonnées polaires (kitxmlcodeinlinelatexdvpr_i,\phi_ifinkitxmlcodeinlinelatexdvp), l'équation d'observation sera :
kitxmlcodelatexdvph_i(X_t) = \left[ \begin{array}{c} \sqrt{(x-x_{ai})^2+(y-y_{ai})^2}\\ atan2(\frac{y_{ai}-y}{x_{ai}-x})-\theta \end{array}\right]finkitxmlcodelatexdvpla matrice jacobienne de l'équation d'observation s'écrira alors :
kitxmlcodelatexdvpH_i=\left[ \begin{array}{ccc} \frac{(x-x_{ai})}{\sqrt{(x-x_{ai})^2+(y-y_{ai})^2}} & \frac{(y-y_{ai})}{\sqrt{(x-x_{ai})^2+(y-y_{ai})^2}} & 0 \\ \frac{(y-y_{ai})}{(x-x_{ai})^2+(y-y_{ai})^2} & - \frac{(x-x_{ai})}{(x-x_{ai})^2+(y-y_{ai})^2} & -1 \end{array} \right]finkitxmlcodelatexdvpPour estimer à la fois la position des amers et du robot, il suffira alors de dérouler les équations du filtrage de Kalman étendu :
- Prédiction de l'état :
kitxmlcodeinlinelatexdvp\begin{equation} X_{t}^* = f(\hat{X}_{t-1},u_t)\quad(11.11) \end{equation}finkitxmlcodeinlinelatexdvp
et de la covariance:
kitxmlcodeinlinelatexdvp\begin{equation} P_t^* = A.\hat{P}_{t-1}.A^T+Q\quad(11.12) \end{equation}finkitxmlcodeinlinelatexdvp - Prédiction de l'observation :
kitxmlcodeinlinelatexdvp\begin{equation} Y_t^*=h(X_t^*)\quad(11.13) \end{equation}finkitxmlcodeinlinelatexdvp - Observation : on obtient une mesure kitxmlcodeinlinelatexdvpYfinkitxmlcodeinlinelatexdvp, dont on estime le bruit kitxmlcodeinlinelatexdvpP_Yfinkitxmlcodeinlinelatexdvp grâce au modèle du processus de perception.
- Correction de l'état prédit:
kitxmlcodeinlinelatexdvp\hat{X}_t = X_t^* + K(Y - Y_t^*)\quad(11.14)finkitxmlcodeinlinelatexdvp kitxmlcodeinlinelatexdvp\hat{P}_t = P_t^* - KHP_t^*\quad(11.15)finkitxmlcodeinlinelatexdvp
où kitxmlcodeinlinelatexdvpKfinkitxmlcodeinlinelatexdvp est le gain de Kalman:
kitxmlcodeinlinelatexdvp\begin{equation} K = P_t^* H^T.(H.P_t^*.H^T + P_Y)^{-1}\quad(11.16) \end{equation}finkitxmlcodeinlinelatexdvp
Cette mise à jour suppose que l'amer perçu soit déjà dans la carte et donc dans le vecteur d'état. Si l'amer détecté par le robot n'est pas dans la carte, il est simplement ajouté à la fin du vecteur d'état et toutes les matrices sont agrandies de deux lignes (et éventuellement colonnes) correspondantes.

Il reste un problème important dans la méthode décrite, car elle suppose que l'on soit capable d'identifier les amers, c'est-à-dire de savoir à quel amer kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp correspond un amer perçu. Or, en utilisant de simples points ou segments de droite, cela se révèle difficile à cause du très fort perceptual aliasing. Comme pour la localisation, il y a deux méthodes possibles pour résoudre ce problème. La première est de particulariser chaque amer, par exemple en utilisant une image de l'environnement autour de l'amer afin de pouvoir l'identifier individuellement. Cette méthode est rarement suffisante, car avec l'augmentation de la taille de l'environnement on retombe en général sur le problème de perceptual aliasing. La seconde solution repose sur des amers indistinguables et sélectionne l'amer correct en se basant sur sa position estimée. Pour cela, on estime la position absolue de l'amer perçu à partir de la position estimée du robot, puis on considère qu'il correspond à l'amer de la carte dont la position est la plus proche. Cette mise en correspondance peut également utiliser une distance de Mahalanobis (voir section III.C.3.c.vApplication à la localisation avec perceptual aliasing), ou utiliser des critères supplémentaires qui caractérisent les amers. Si les amers sont des segments, par exemple, on peut chercher le segment le plus proche qui a la même direction que le segment perçu.
L'algorithme 11.2 décrit finalement le processus complet de cette méthode de cartographie. Cette méthode est également illustrée graphiquement dans la Figure 11.10.
La principale faiblesse de cette méthode réside dans la phase d'appariement qui peut entraîner une divergence de l'algorithme en cas d'erreur. En effet, dans ce cas, non seulement la position de l'amer apparié par erreur sera mal estimée, mais cette mauvaise estimation sera propagée aux autres amers, via la matrice des covariances, ainsi qu'à la position du robot. Cette mauvaise estimation de la position du robot produira par la suite de nouvelles erreurs d'appariement qui se succéderont et entraîneront la divergence complète de l'algorithme.
Un autre inconvénient est la complexité des calculs requis, qui augmente en kitxmlcodeinlinelatexdvpO(N^2)finkitxmlcodeinlinelatexdvp avec le nombre d'amers de la carte. Ceci est lié à la taille de la matrice de covariances qui est kitxmlcodeinlinelatexdvpN\times Nfinkitxmlcodeinlinelatexdvp. Or cette matrice mémorise les interrelations entre les positions des amers et du robot et est nécessaire à la bonne estimation de ces positions.
Pour réduire la complexité des calculs, il est cependant possible de réduire la taille de cette matrice en négligeant certaines interrelations entre amers. Ceci peut se faire par exemple en ne mémorisant les covariances qu'au sein de cartes locales, dont l'assemblage couvre l'ensemble de l'environnement. Diverses méthodes existent, utilisant différentes manières de découper la carte globale et de propager les informations entre cartes locales (par exemple [109]).
IV-D-3-c. Fast SLAM▲
La méthode d'appariement des amers utilisée dans la méthode du SLAM EKF est à la source de la plupart des problèmes de cette méthode. Elle repose en effet sur l'hypothèse que l'estimation de la position du robot est approximativement correcte pour fournir un appariement correct. On peut donc remarquer que si la position du robot est parfaitement connue, le problème se simplifie énormément, car la mise en correspondance ne pose plus de problème et il reste simplement à estimer correctement la position des amers, ce qui est relativement trivial (sous l'hypothèse de la connaissance de la position du robot).
Cette remarque a inspiré la méthode de cartographie nommée Fast SLAM [100, 70, 60]. Dans cette méthode, on mémorise un grand nombre de trajectoires possibles, dont on évalue la probabilité, et pour ces trajectoires, on construit simplement la carte à partir des perceptions. Cet ensemble de trajectoires correspond en fait à un échantillonnage de la distribution de probabilités sur ces trajectoires au moyen d'un filtre particulaire. Pour la construction de la carte à partir de l'une de ces trajectoires, on utilise le filtrage de Kalman, mais dans des conditions beaucoup plus favorables. En effet, comme la trajectoire est connue, les perceptions successives des différents amers deviennent indépendantes et il n'est plus nécessaire de mémoriser l'ensemble des covariances, mais seulement les variances des amers individuels. On passe ainsi d'une complexité en kitxmlcodeinlinelatexdvpO(N^2)finkitxmlcodeinlinelatexdvp à une complexité en kitxmlcodeinlinelatexdvpO(N)finkitxmlcodeinlinelatexdvp pour la partie filtrage de Kalman. Il faut cependant y ajouter la complexité du filtrage particulaire sur les trajectoires, mais globalement, l'algorithme est plus stable et moins gourmand en calculs que le SLAM original.
Cette méthode de séparation du problème de SLAM et un filtre particulaire pour la partie non gaussienne et en un filtre de Kalman pour une partie du sous-problème est une méthode très générale connue sous le nom de Rao-Blackwellisation du filtre.
|
Figure 11.11 - Avant la fermeture d'un cycle, un très grand nombre de trajectoires sont évaluées. Après fermeture, le filtre particulaire sur les trajectoires sélectionne automatiquement celle correspondant effectivement au cycle (image tirée de [70]). |
La force de ces méthodes est surtout apparente lors de la fermeture de grands cycles. En effet, avant la fermeture, un grand nombre de trajectoires différentes sont mémorisées, ce qui permet d'avoir une forte probabilité que l'une d'elles corresponde à la trajectoire précise du cycle. Après la fermeture du cycle, le rééchantillonnage du filtre particulaire sélectionne naturellement les trajectoires correctes et permet ainsi une cartographie correcte du cycle (Figure 11.11). Ce rééchantillonnage entraîne cependant une forte perte d'informations, puisque la plupart des trajectoires estimées avant la fermeture de boucle sont ignorées (c'est le problème classique de raréfaction des particules des méthodes de filtrage particulaire, voir section III.C.4.dFiltrage particulaire). Cette perte d'informations devient problématique dans des environnements contenant plusieurs cycles, notamment dans le cas de cycles imbriqués.
|
Figure 11.12 - Exemple de carte construite par la méthode du FastSLAM. Cette carte contient de nombreux couloirs et plusieurs boucles et représente donc un problème difficile pour le SLAM (image tirée de [60]). |
Une méthode de cartographie très similaire au FastSLAM permet de construire une carte métrique directement à partir des données laser [70]. Elle n'utilise pas de filtre de Kalman, mais repose sur un échantillonnage des trajectoires possibles par un filtre particulaire et sur un algorithme rapide de corrélation de scans pour l'évaluation des probabilités des trajectoires. Cette méthode permet de construire de très grandes cartes contenant plusieurs cycles (Figure 11.12).
IV-D-4. Comparaison des méthodes de cartographie▲
Les méthodes de cartographie les plus simples sont les méthodes de cartographie incrémentales topologiques, elles montrent cependant rapidement leurs limites en termes de robustesse et demandent souvent une mise au point importante pour obtenir une capacité de reconnaissance de nœuds suffisamment fiables.
Concernant la cartographie métrique, les méthodes de corrélation de scans laser et de grille d'occupation sont également assez simples à mettre en œuvre et sont suffisantes pour des environnements de taille restreinte, ne contenant notamment pas trop de cycles. Elles sont donc très populaires.
Les méthodes de SLAM seront en général plus efficaces, mais plus complexes à mettre en œuvre. La version basique du SLAM utilisant un filtre de Kalman reste cependant assez simple, mais au prix d'un manque de robustesse en cas de mauvaises perceptions ou de mauvaise odométrie et d'une grande sensibilité à la qualité de l'association de données. Le FastSLAM quant à lui est plus complexe, mais apporte de réels gains de robustesse, il est cependant limité par le problème de raréfaction des particules qui devient problématique pour les environnements de grande taille contenant plusieurs cycles.
IV-D-5. Pour aller plus loin▲
Les archives de la « SLAM summer school » de 2002 contenant de nombreux articles et tutoriels :
Un site regroupant de nombreux algorithmes de SLAM en open source :
Le livre Probabilitic Robotics de Sebastian Thrun, Wolfram Burgard et Dieter Fox [135] détaille de manière très précise l'ensemble des algorithmes de SLAM.
IV-E. Planification▲
Connaissant une carte de l'environnement et la position du robot au sein de cette carte, il est possible de calculer une trajectoire pour rejoindre un but. Nous décrirons dans ce chapitre quelques méthodes simples pour la planification restreinte à des déplacements en 2D. Pour un aperçu plus large des techniques de planification, on pourra par exemple se reporter à [88] ou [90].
IV-E-1. Espace des configurations▲
Dans le cadre de ce cours, nous considérons des robots capables de se déplacer dans un espace à deux dimensions dont les commandes influent avec des relations simples sur la position dans cet espace (via la vitesse et la direction). Le calcul des déplacements peut donc se faire directement dans l'espace de la carte, en évitant seulement les positions qui conduiraient à des collisions avec les obstacles. Dans un cadre plus général, la planification est plutôt réalisée dans l'espace des degrés de liberté du robot appelé espace des configurations (qui peut être beaucoup plus grand que l'espace des mouvements, par exemple pour un bras manipulateur). Les obstacles de l'espace des déplacements sont alors traduits dans l'espace des configurations par des kitxmlcodeinlinelatexdvpCfinkitxmlcodeinlinelatexdvp ¬ obstacles qui correspondent aux configurations des degrés de liberté qui vont faire percuter un obstacle au robot.
|
Figure 12.1 - Illustration de l'espace des configurations dans le cas 2D. Gauche : Carte des obstacles. Droite : espace des configurations contenant les positions accessibles au robot sans percuter les obstacles (en blanc). |
Dans le cas 2D pour un robot holonome, l'espace des configurations que nous utiliserons sera donc simplement l'espace de travail auquel nous enlèverons toutes les positions conduisant à percuter un obstacle (Figure 12.1), c'est-à-dire les obstacles eux-mêmes, plus une marge de sécurité autour des obstacles correspondant au rayon du robot.
IV-E-2. Discrétisation de l'espace de recherche▲
Les algorithmes de planification utilisent en général des méthodes de recherche de chemin dans des graphes. Il faut donc représenter la carte sous la forme d'un graphe. Les cartes topologiques fournissent directement ce graphe, mais dans le cas des cartes métriques, qui représentent l'espace de manière continue, ces techniques ne sont utilisables qu'après discrétisation de l'espace libre représenté dans la carte. Pour ce faire, certains modèles intègrent directement cette décomposition au niveau de la cartographie, en construisant une carte topologique parallèlement à la carte métrique [5, 29, 131, 22]. D'autres modèles font appel à des décompositions de l'espace libre spécifiques à la planification. Notons qu'il existe également des techniques, tels les champs de potentiel analogues à ceux décrits dans le chapitre sur la navigation réactive [87, 38, 104] qui permettent de calculer des chemins directement dans le domaine continu, sans phase préalable de discrétisation. Nous n'aborderons cependant pas ces techniques dans ce cours.
Il existe deux catégories de méthodes pour discrétiser l'espace de recherche des cartes métriques. Les méthodes de la première catégorie font appel à des décompositions en cellules, de différents types, qui permettent de représenter la topologie de l'espace libre [87, 104] (cf. Figure 12.2). La décomposition exacte permet de représenter l'ensemble de l'espace libre, à l'aide de cellules de formes irrégulières qui joignent les sommets des obstacles. La décomposition en cellules régulières pave l'espace libre de carrés, surestimant donc la surface des obstacles, ce qui peut être gênant si les cellules sont grandes. Ce type de représentation peut aussi correspondre en pratique à une grille d'occupation pour laquelle ce problème ne se pose pas. Enfin une représentation hiérarchique telle que le « quadtree » permet d'utiliser des cellules de tailles variables en fonction de la complexité locale de l'environnement et de représenter donc finement l'espace libre tout en limitant l'occupation mémoire. Les cellules obtenues sont ensuite utilisées de manière similaire aux nœuds des cartes topologiques dans le processus de planification, les cellules adjacentes étant considérées comme reliées par une arête.
Les méthodes de la seconde catégorie font appel au précalcul de chemins entre des points répartis dans l'environnement [87, 88] (cf. Figure 12.3). Le graphe de visibilité utilise les angles d'obstacles qui sont les points que le robot devra contourner pour éviter ces obstacles. Le diagramme de Voronoï utilise les points équidistants de plusieurs obstacles qui permettent de générer des chemins passant le plus loin possible des obstacles. La méthode « Rapidly exploring Random Trees » [89] quant à elle, construit un arbre aléatoirement en vérifiant que les branches créées ne rencontrent pas les obstacles. Cette méthode est très efficace, car elle permet d'échantillonner l'espace sans le parcourir de manière exhaustive et peut aussi prendre en compte les contraintes de non-holonomie du robot. Les points sont ensuite utilisés comme les nœuds d'une carte topologique, tandis que les chemins précalculés reliant les nœuds seront utilisés comme les arêtes de cette carte.
La planification du chemin entre deux points de l'environnement se réalise alors en deux étapes. La première étape permet de calculer un chemin direct entre, d'une part, le point de départ et le point le plus proche dans l'espace discrétisé et, d'autre part, le point de l'espace discrétisé le plus proche du but et le but en question. La seconde étape permet ensuite de calculer un chemin entre ces deux points de l'espace discrétisé, en utilisant une des méthodes décrites dans le prochain paragraphe. Ces trois parties de trajectoires sont ensuite assemblées pour obtenir le chemin reliant le point de départ au but. Une phase d'optimisation supplémentaire peut être utilisée pour limiter les effets de la discrétisation et lisser la trajectoire (cf. Figure 12.4). Dans le cas de la décomposition de l'espace libre en cellules, les points de l'espace discrétisé utilisés peuvent être les centres des cellules ou les milieux des côtés des cellules. Dans le cas de l'utilisation de chemins précalculés, ces points sont simplement les points de passage de ces chemins.
IV-E-3. Recherche de chemin▲
À partir d'une carte métrique discrétisée ou d'une carte topologique représentée sous forme d'un graphe, il existe différentes méthodes pour calculer un chemin entre la cellule de départ et la cellule but. Nous distinguons ici les méthodes selon le type de plan qu'elles génèrent.
IV-E-3-a. Deux types de plan▲
Le premier type de plan qui peut être généré contient une suite d'actions à effectuer par le robot, ou une suite de points à atteindre afin de rejoindre le but. Les algorithmes classiques de recherche dans les graphes, tels que l'algorithme de Dijkstra, kitxmlcodeinlinelatexdvpA^\starfinkitxmlcodeinlinelatexdvp, ou l'une de leurs nombreuses variantes, peuvent être utilisés pour calculer ce type de plan [93, 79, 81, 120, 106, 5, 38]. La taille raisonnable des cartes topologiques classiquement utilisées en robotique rend ces algorithmes suffisamment efficaces en pratique. Ce type de plan pose toutefois des problèmes lors de son exécution si le robot ne parvient pas à atteindre l'un des points du chemin calculé, ou s'il s'éloigne de la trajectoire et que sa position correspond à un nœud qui ne fait pas partie du chemin planifié. La solution à ces problèmes est alors de recommencer le processus de planification en prenant en compte la nouvelle position de départ (ce qui peut même se produire indéfiniment en cas de problème). Ce processus de replanification est souvent inutilement coûteux en calculs, car un grand nombre des opérations nécessaires auront déjà été effectuées lors de la planification précédente.
Un second type de plan peut être utilisé, qui associe à chacune des positions possibles du robot au sein de la carte l'action qu'il doit effectuer pour atteindre son but. Ce type de plan est appelé politique (comme pour l'apprentissage par renforcement, section II.CApprentissage par renforcement) ou plan universel [121]. Le résultat est alors une stratégie de déplacement similaire à la stratégie d'action associée à un lieu mentionnée dans la section I.A.1Stratégies de navigation. L'enchaînement de reconnaissances de positions et de réalisations des actions associées à ces positions permet donc de générer une route joignant le but. Ce type de plan présente l'avantage de permettre au robot d'atteindre le but, aussi longtemps qu'il possède une estimation correcte de sa position. En effet, le chemin précis rejoignant le but n'est pas spécifié et le robot peut donc s'écarter du chemin direct entre la position initiale et le but sans entraîner de replanification.
Une politique est plus lourde à calculer que les plans du type précédent, car toutes les positions de la carte doivent être envisagées, sans utiliser les heuristiques des algorithmes précédents qui permettent de restreindre l'exploration de l'espace de recherche. Toutefois, cette augmentation est rapidement compensée si le robot s'écarte du chemin direct vers le but. Dans ce cas, en effet, la planification doit être reprise pour le premier type de plan, alors que c'est inutile pour une politique. Le calcul d'une politique reste donc en général praticable pour les cartes de taille limitée typiques de la robotique mobile.
IV-E-3-b. Calcul de politique▲
Pour calculer une telle politique, une simple recherche en largeur dans le graphe en partant du but peut être utilisée. Cette méthode se retrouve sous le nom de breadth first search, spreading activation [98, 10] ou wavefront propagation [104]. Ces deux derniers noms viennent de l'analogie entre l'ordre de parcours du graphe et la manière dont un fluide progresserait s'il s'échappait du but pour se répandre dans le graphe.
Plutôt que d'associer directement une action à chaque état, le calcul d'une politique passe souvent par le calcul d'un potentiel associé à chaque état qui augmente en fonction de la distance nécessaire pour atteindre le but depuis l'état courant. À partir de ce potentiel, il est alors très simple de retrouver les actions à effectuer par une simple descente de gradient.
Pour calculer ce potentiel, des coûts élémentaires sont associés à chaque nœud et à chaque lien entre les nœuds. Les coûts associés aux liens traduisent en général la distance entre nœuds, tandis que les coûts associés aux nœuds permettent de marquer des zones à éviter ou à favoriser pour les trajectoires du robot.

La méthode la plus simple pour calculer le potentiel est l'algorithme de Dijkstra (12.1), qui, partant du but fait à chaque étape la mise à jour du nœud suivant de potentiel le plus faible. Cet algorithme suppose que tous les coûts utilisés sont positifs ou nuls.
Une seconde méthode pour calculer ces potentiels lorsque certains coûts sont négatifs est l'utilisation de l'algorithme de programmation dynamique de Bellman-Ford (12.2), aussi connu sous le nom de value iteration, notamment en apprentissage par renforcement [22, 131, 23]. Une itération de cet algorithme utilise quasiment la même méthode de mise a jour que l'algorithme de Dijkstra, mais sans utiliser le même ordre dans les mises à jour des nœuds. En présence de coûts négatifs, cette itération doit être répétée autant de fois qu'il y a de nœuds pour garantir la convergence. De plus il peut arriver qu'un cycle du graphe ait un poids total négatif, ce qui ne permet pas de trouver de chemin de coût minimal. L'algorithme retourne FAUX dans ce cas.
|
Figure 12.5 - Propagation des valeurs de potentiel selon l'algorithme utilisé. Les poids associés aux nœuds (ici les cases d'une grille d'occupation) sont nuls, et les poids des liens sont la distance entre deux nœuds. La rangée du haut montre les résultats de l'algorithme de Dijkstra, celle du bas ceux de Value Iteration. |
La Figure 12.5 permet de comparer l'ordre des mises à jour des valeurs de potentiels pour l'algorithme de Dijkstra et pour Value Iteration, qui aboutissent au même résultat.
IV-E-3-c. Calcul d'un chemin▲
Si l'on ne souhaite que calculer un chemin, il est par exemple possible d'employer l'algorithme kitxmlcodeinlinelatexdvpA^\starfinkitxmlcodeinlinelatexdvp. Cet algorithme utilise exactement le même mécanisme que l'algorithme de Dijkstra, mais utilise une heuristique pour choisir le nœud suivant à explorer au lieu d'explorer systématiquement les nœuds voisins des nœuds déjà planifiés. Cette heuristique doit fournir une évaluation la plus rapide possible de la distance entre le nœud courant et le but (par exemple simplement la distance euclidienne en supposant qu'il n'y a pas d'obstacle). La mise en place d'une bonne heuristique assure de trouver très rapidement un chemin vers le but, mais ne garantit pas forcément l'optimalité (ce qui n'est souvent pas très important en pratique).
IV-E-4. Exemples de politiques▲
|
|
|
|
|
Figure 12.6 - Gauche : Potentiel et exemple de trajectoires avec des poids de liens égaux à la distance entre nœuds. Centre : Poids associé aux nœuds fonction de la distance aux obstacles. Droite : Exemples de trajectoires obtenues en utilisant les poids de l'image du centre. |
||
La Figure 12.6 donne à gauche un exemple de champ de potentiel obtenu en utilisant un poids nul pour les nœuds et la distance entre nœuds comme poids sur les liens. Avec ce type de carte, ce choix pose le problème de générer des trajectoires très proches des obstacles, qui peuvent être dangereuses pour le robot.
Pour éviter ce problème, il est possible d'associer un poids dépendant de la distance à l'obstacle le plus proche à chacun des nœuds. Ceci a pour but de pénaliser les trajectoires proches des murs et de guider le robot selon l'axe des couloirs au lieu de longer un des murs. La Figure 12.6 montre à droite le poids associé aux nœuds et les trajectoires obtenues.
IV-E-5. Choix de l'action avec une position incertaine▲
Lorsque la position estimée par le système de localisation est non ambiguë, l'utilisation d'une politique se résume simplement au choix de l'action associée avec la position courante. Toutefois, les systèmes réalisant le suivi de plusieurs hypothèses fournissent également une estimation de la probabilité de présence du robot en différentes positions. Il peut donc se révéler utile de tenir compte de ces probabilités pour sélectionner l'action à exécuter.
|
Figure 12.7 - Exemple de l'intérêt d'une procédure de vote dans le cas où la situation du robot est incertaine. Si l'on choisit l'action associée à la position la plus probable, le robot ira en haut, ce qui correspondra à l'action correcte avec une probabilité kitxmlcodeinlinelatexdvp0,2finkitxmlcodeinlinelatexdvp. En utilisant une méthode de vote, l'action choisie sera d'aller à droite, ce qui sera correct avec une probabilité kitxmlcodeinlinelatexdvp0,8finkitxmlcodeinlinelatexdvp. |
Différentes méthodes permettent de prendre ces probabilités en compte. Une première méthode consiste à utiliser une méthode de vote [127, 27]. Pour cela, une action est simplement associée à chacun des nœuds de la carte, en utilisant une des méthodes décrites au paragraphe précédent. Un score est alors calculé pour chaque action. Ce score est la somme des probabilités des nœuds auxquels chaque action est associée. L'action ayant le score le plus élevé est alors exécutée. Cette méthode est efficace dans les cas de grande ambiguïté dans la localisation, où la probabilité de la position la plus probable est seulement très légèrement supérieure aux autres. Dans ce cas, en effet, si la direction associée à la position la plus probable est incorrecte, cette méthode permet de l'ignorer et de choisir une direction associée à plusieurs autres hypothèses de position qui se révélera correcte dans un plus grand nombre de cas (cf. Figure 12.7).
La méthode précédente tente de diriger le robot vers le but, quelle que soit l'incertitude de l'estimation de sa position. Or si cette estimation est très incertaine, il est souvent plus judicieux de chercher d'abord à mieux l'estimer avant de chercher à rejoindre le but. Il est ainsi possible de mesurer la confiance dans l'estimation courante de la position pour choisir une action. Cette confiance peut être simplement mesurée par l'entropie de la distribution de probabilités [27, 132]. Ainsi, si l'entropie de la distribution de probabilités représentant la position est trop élevée, une action permettant de diminuer cette entropie sera sélectionnée. L'utilisation de telles stratégies permet par exemple d'éviter des zones dans lesquelles l'incertitude de localisation est plus grande (par exemple les larges espaces ouverts), et de privilégier les zones plus favorables à l'estimation de la position (par exemple les zones où se trouvent des points de repère fiables). Cette méthode a été présentée sous le nom de « Coastal Navigation » [115].